Untergruppen, Untergruppenkriterien: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Gegenbeispiel 2) |
K (→Zeigen, dass e \in U) |
||
| (11 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 147: | Zeile 147: | ||
==Satz: (triviale Untergruppen)== | ==Satz: (triviale Untergruppen)== | ||
::Jede Gruppe hat wenigstens zwei Untergruppen: Sich selbst und die Untergruppe die nur aus dem Einselement der Gruppe besteht. | ::Jede Gruppe hat wenigstens zwei Untergruppen: Sich selbst und die Untergruppe die nur aus dem Einselement der Gruppe besteht. | ||
| + | =Untergruppenkriterium 1= | ||
| + | ==Satz: (Untergruppenkriterium 1)== | ||
| + | ::Es sei <math>[G, \circ]</math> eine Gruppe und <math>U \subseteq G</math>. <math>[U, \circ]</math> ist genau dann Untergruppe von <math>[G, \circ]</math>, wenn: | ||
| + | :::<math> | ||
| + | \begin{matrix} | ||
| + | \text{(I)} & \forall a,b \in &U & : & a \circ b &\in U \\ | ||
| + | \text{(II)} & \forall a \in &U & : & a^{-1} &\in U | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | =Untergruppenkriterium 2= | ||
| + | ==Satz (Untergruppenkriterium 2)== | ||
| + | ::Es sei <math>[G, \circ]</math> eine Gruppe und <math>U \subseteq G. ~</math> <math>~[U, \circ]</math> ist genau dann Untergruppe von <math>[G, \circ]</math>, wenn: | ||
| + | :::<math> | ||
| + | \forall a,b \in U : a \circ b^{-1}\in U </math> | ||
| + | ==Beweis von UGK 2== | ||
| + | Wenn UGK1 bewiesen wurde (was keine Schwierigkeit darstellt) reicht es zu zeigen, dass <math>\text{UGK1} \Leftrightarrow \text{UGK2}</math> gilt.<br /> | ||
| + | ===<math>\rightarrow</math>=== | ||
| + | trivial | ||
| + | ===<math>\leftarrow</math>=== | ||
| + | Es sei <math>[G, \circ]</math> eine Gruppe mit Einselement <math>e</math>. <math>U \subseteq G</math>. | ||
| + | ====Voraussetzung==== | ||
| + | <math>\text{(*)}~\forall a, b \in U: a\circ b^{-1}\in U</math>. | ||
| + | ====Behauptungen==== | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | \text{(I)} & \forall a, b \in U: & a \circ b \in U \\ | ||
| + | \text{(II)} & \forall b \in U: & b^{-1} \in U | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | ====Beweis==== | ||
| + | =====Zeigen, dass <math>e \in U</math>===== | ||
| + | <math>\text{(*)}</math> sagt aus, dass mit <math>a</math> und <math>b</math> aus der Teilmenge <math>U</math> auch das Produkt <math>a \circ b^{-1}</math> ein Element von <math>U</math> ist.<br /> | ||
| + | Setzen <math>b=a</math>, womit nach <math>\text{(*)}~ a\circ a^{-1} \in U</math> gilt. Wegen <math>a \circ a^{-1} =e</math> ist das Einselement <math>e</math> ein Element der Teilmenge <math>U</math>. | ||
| + | |||
| + | =====Zeigen, dass mit <math>b</math> auch <math>b^{-1}</math> zu <math>U</math> gehört===== | ||
| + | Wegen <math>e \in U</math> (gerade gezeigt) und <math>b \in U</math> (Voraussetzung) gilt nach <math>\text{(*)}</math> <math>e \circ b^{-1} = b^{-1} \in U</math>. <br /> | ||
| + | <math>\text{(II)}</math> ist damit bewiesen. | ||
| + | |||
| + | =====Zeigen, dass die Verknüpfung <math>\circ</math> abgeschlossen auf <math>U</math> ist===== | ||
| + | Wir haben gerade gezeigt, dass mit <math>b \in U</math> auch <math>b^{-1} \in U</math> gilt.<br /> | ||
| + | Mit <math>a \in U</math> und <math>b^{-1} \in U</math> gilt nach <math>\text{(*)}</math> <math>a \circ \left ( b^{-1} \right ) ^{-1} \in U</math>.<br /> | ||
| + | Nach einem Hilfssatz aus der Vorlesung gilt: <math>\left ( b^{-1} \right ) ^{-1} = b</math> und damit <math>a \circ b \in U</math>, womit <math>\text{(I)}</math> bewiesen wurde. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 14. Juli 2018, 13:30 Uhr
Beispiele, GegenbeispieleBeispiel 1Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus
Wir wählen aus
Beispiel 2Die Gruppe der BewegungenDie GruppenmitgliederUnter einer Bewegung
|
![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.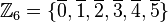




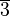
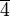
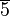
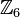 die folgende Teilmenge
die folgende Teilmenge 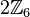 aus:
aus: 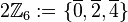
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von
ist eine Gruppe und damit eine Untergruppe von  versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
versteht man eine abstandserhaltende Abbildung der Ebene auf sich: unsere Ebene.
unsere Ebene.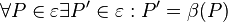
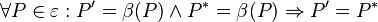
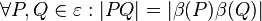
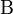 bezeichnen.
bezeichnen.
 .
.
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe
ist Gruppe und
und 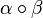 eine Bewegung ist.
eine Bewegung ist.
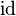 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
, die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: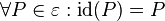
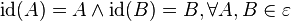 gilt natürlich auch
gilt natürlich auch 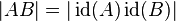 .
.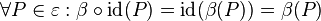 und somit
und somit 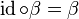 .
.
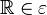 bei
bei 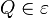 hat.
hat.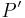 das Bild von
das Bild von  bei der Bewegung
bei der Bewegung 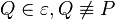 gibt, der durch
gibt, der durch  gibt. Dann gilt:
gibt. Dann gilt: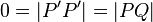 und damit
und damit 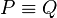 , was ein Widerspruch zur Annahme
, was ein Widerspruch zur Annahme 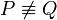 ist.
ist.
 und
und  aus
aus  abgebildet werden:
abgebildet werden: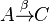
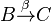
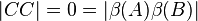 müssen
müssen 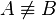 . Unsere Annahme
. Unsere Annahme  besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt
besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt 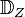 die Menge aller Drehungen um
die Menge aller Drehungen um ![[\mathbb{D}_Z, \circ ]](/images/math/5/5/2/552d0d83fed54a94d1775beb5f9391f9.png) ist eine Gruppe:
ist eine Gruppe:
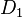 und
und 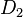 zwei Drehungen um
zwei Drehungen um 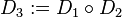 ebenfalls eine Bewegung. Weil
ebenfalls eine Bewegung. Weil 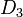 sein. Es können jetzt genau zwei Fälle auftreten:
sein. Es können jetzt genau zwei Fälle auftreten:
 .
.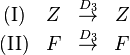
 der Geraden
der Geraden 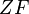 ist ein Fixpunkt bei
ist ein Fixpunkt bei 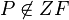 . Für das Bild
. Für das Bild 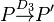
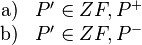
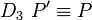 , woras folgt, dass jeder Punkt der Ebene bei
, woras folgt, dass jeder Punkt der Ebene bei 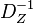 zu einer Bewegung
zu einer Bewegung 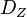 mit genau dem Fixpunkt
mit genau dem Fixpunkt ![[\mathbb{Z}_7, \oplus ]](/images/math/4/f/9/4f99ed9383011693e47f2407152b959a.png) und
und ![[\mathbb{Z}_7, \otimes ]](/images/math/3/e/6/3e625be0a151457aeba319347851fb4b.png) . Da wir bei multiplikativen Restgruppen das neutrale Element bezüglich der Restklassenaddition nicht berücksichtigen ist die Menge der multiplikativen Restklassengruppe modulo
. Da wir bei multiplikativen Restgruppen das neutrale Element bezüglich der Restklassenaddition nicht berücksichtigen ist die Menge der multiplikativen Restklassengruppe modulo 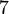 eine echte Teilmenge der additiven Restklassengruppe modulo
eine echte Teilmenge der additiven Restklassengruppe modulo ![[\mathbb{Z}_4, \oplus ]](/images/math/8/0/9/809eadba6a0a17ba00b6356273a6aade.png) ist bekannterweise eine Gruppe.
ist bekannterweise eine Gruppe. ![[T, \oplus]](/images/math/b/6/7/b67f906e0eb5b26fdf8bc244b095c477.png) mit
mit 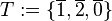 ist keine Untergruppe von
ist keine Untergruppe von ![[G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe und
eine Gruppe und 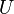 eine Teilmenge von
eine Teilmenge von ![[U, \circ ]](/images/math/b/e/9/be91aec2753430c87cc11578aed000df.png) ist Untergruppe von
ist Untergruppe von 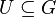 .
. 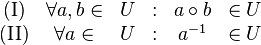
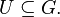
![~[U, \circ]](/images/math/7/8/2/782ef8008e3aad3a582c61112602da9d.png) ist genau dann Untergruppe von
ist genau dann Untergruppe von 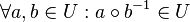
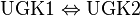 gilt.
gilt.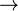

 .
. 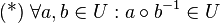 .
.
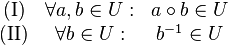
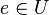
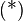 sagt aus, dass mit
sagt aus, dass mit  und
und  aus der Teilmenge
aus der Teilmenge 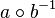 ein Element von
ein Element von 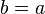 , womit nach
, womit nach 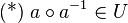 gilt. Wegen
gilt. Wegen 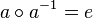 ist das Einselement
ist das Einselement 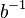 zu
zu 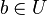 (Voraussetzung) gilt nach
(Voraussetzung) gilt nach 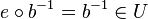 .
. 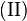 ist damit bewiesen.
ist damit bewiesen.
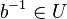 gilt.
gilt.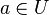 und
und 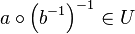 .
.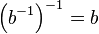 und damit
und damit 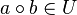 , womit
, womit 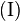 bewiesen wurde.
bewiesen wurde.

