Lösung von Aufgabe 9.5P (WS 18/19): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\…“) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ''m'' sei Mittelsenkrechte der Strecke <math>\overline{AB}</math>. Beweisen Sie durch Kontraposition: <math>\left| AP \right| =\left| BP \right|\Rightarrow P\in m</math> | ||
<br />Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung. <br />Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.<br /> | <br />Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung. <br />Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.<br /> | ||
| − | + | <br /> | |
| + | Vor.: P <s>ε</s> m Beh: => |AP|≠|PB|<br /> | ||
| + | 1.) P<s>ε</s> m => entweder P ε mA<sup>+</sup> oder P ε mA<sup>-</sup>. '''- Vor'''<br /> | ||
| + | 2.) m geschnitten <math>\overline{AB}</math> ≠ {} => entweder m geschnitten <math>\overline{AP}</math> ≠ {} oder m geschnitten <math>\overline{PB}</math> ≠ {}. '''- 1.), Satz von Pasch'''<br /> | ||
| + | 3.) Für P ε mA<sup>+</sup> (und m geschnitten <math>\overline{PB}</math> ≠ {})<br /> | ||
| + | m geschnitten <math>\overline{PB}</math> = {S}. '''- 2.), Anmerkung 3.''')<br /> | ||
| + | 4.) Für das Dreieck <math>\overline{ASP}</math> gilt |AP| < |AS| + |SP|. '''- Dreiecksungleichung'''<br /> | ||
| + | 5.) S<sub>m</sub>(A) = B => |AS| = |BS|. '''- Streckentreue, Längenerhaltung'''<br /> | ||
| + | 6.) |PB| = |PS| + |SB|. '''- 3.), 5.)'''<br /> | ||
| + | 7.) |PB| = |PS| + |AS|. '''- 5.), 6.)'''<br /> | ||
| + | 8.) ( |AP| < |AS| + |AP| ) = ( |AP| < |PB| ). '''- 4.), 7.)'''<br /> | ||
| + | => |AP| ≠ |PB|. Die Behauptung und somit auch das logische Äquivalent stimmt.<br /> | ||
| + | --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 13:52, 14. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 14. Dezember 2018, 13:52 Uhr
m sei Mittelsenkrechte der Strecke 
. Beweisen Sie durch Kontraposition: 
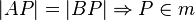
Tipp: Nutzen Sie den Satz von Pasch und die Dreiecksungleichung.
Hinweis: Die Umkehrung des hier zu beweisenden Satzes sei bereits bewiesen.
Vor.: P ε m Beh: => |AP|≠|PB|
1.) Pε m => entweder P ε mA+ oder P ε mA-. - Vor
2.) m geschnitten ≠ {} => entweder m geschnitten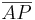 
≠ {} oder m geschnitten 
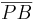≠ {}. - 1.), Satz von Pasch
3.) Für P ε mA+ (und m geschnitten ≠ {})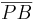
m geschnitten 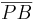= {S}. - 2.), Anmerkung 3.)
4.) Für das Dreieck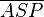 
gilt |AP| < |AS| + |SP|. - Dreiecksungleichung
5.) Sm(A) = B => |AS| = |BS|. - Streckentreue, Längenerhaltung
6.) |PB| = |PS| + |SB|. - 3.), 5.)
7.) |PB| = |PS| + |AS|. - 5.), 6.)
8.) ( |AP| < |AS| + |AP| ) = ( |AP| < |PB| ). - 4.), 7.)
=> |AP| ≠ |PB|. Die Behauptung und somit auch das logische Äquivalent stimmt.
--CIG UA (Diskussion) 13:52, 14. Dez. 2018 (CET)
