Lösung von Aufgabe 8.2P (WS 18 19): Unterschied zwischen den Versionen
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 10: | Zeile 10: | ||
Die Strecke "Augen-B'" ist genau so lang, wie "Augen-S2-Kopf", die somit auch kürzeste Verbindung der beiden Punkte über h (Spiegel) ist. Analgog ist "Augen-A'" genau so lang wie "Augen-S1-Füße", also ebenfalls die kürzese Verbindung über den Spiegel. Anders formuliert muss der Spiegel die Strecke "S1-S2" abdecken.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:00, 14. Dez. 2018 (CET) | Die Strecke "Augen-B'" ist genau so lang, wie "Augen-S2-Kopf", die somit auch kürzeste Verbindung der beiden Punkte über h (Spiegel) ist. Analgog ist "Augen-A'" genau so lang wie "Augen-S1-Füße", also ebenfalls die kürzese Verbindung über den Spiegel. Anders formuliert muss der Spiegel die Strecke "S1-S2" abdecken.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 11:00, 14. Dez. 2018 (CET) | ||
wie ist denn das Verhältnis von <math>\left| S_1S_2 \right|</math> zu <math>\left| A'B' \right|</math>?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:08, 17. Dez. 2018 (CET) | wie ist denn das Verhältnis von <math>\left| S_1S_2 \right|</math> zu <math>\left| A'B' \right|</math>?--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:08, 17. Dez. 2018 (CET) | ||
| − | S<sub>1</sub>S<sub>2</sub> ist halb so groß wie A'B'. Wenn wir einen Punkt X auf Höhe der Augen zwischen S<sub>1</sub> und S<sub>2</sub> anbringen, dann gilt: |XS<sub>2</sub>| ist halb so groß wie |XB'| und |XS<sup>1</sup>| ist halb so groß wie |XA'|, somit ist |S<sub>1</sub>S<sub>2</sub>| halb so groß wie |A'B'|.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:44, 20. Dez. 2018 (CET) | + | |S<sub>1</sub>S<sub>2</sub>| ist halb so groß wie |A'B'|. Wenn wir einen Punkt X auf Höhe der Augen zwischen S<sub>1</sub> und S<sub>2</sub> anbringen, dann gilt: |XS<sub>2</sub>| ist halb so groß wie |XB'| und |XS<sup>1</sup>| ist halb so groß wie |XA'|, somit ist |S<sub>1</sub>S<sub>2</sub>| halb so groß wie |A'B'|.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 20:44, 20. Dez. 2018 (CET) |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 20. Dezember 2018, 20:44 Uhr
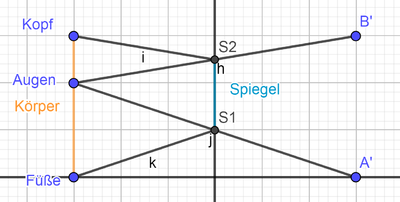
Wie hoch muss ein Spiegel sein, damit Sie sich ganz darin sehen können und auf welcher Höhe muss die Oberkante des Spiegels angebracht werden? Anmerkung: Sie dürfen hier die Strahlensätze, wie sie aus der Schule bekannt sind, verwenden. Tipp: Hier finden Sie eine hilfreiche GeoGebra-Applikation.
Der Spiegel muss so hoch hängen, dass er ab der Mitte der Strecke Füße-Augen anfängt, die Oberkante liegt bei der Mitte der Strecke Augen-Kopf (mit Kopf ist der oberste Teil des Kopfes gemeint).--CIG UA (Diskussion) 22:03, 6. Dez. 2018 (CET)
ok, die Zeichnung erklärt das Ganze schon sehr schön, können Sie das auch mathematisch formal korrekt begründen?--Schnirch (Diskussion) 11:55, 10. Dez. 2018 (CET)
Die Strecke "Augen-B'" ist genau so lang, wie "Augen-S2-Kopf", die somit auch kürzeste Verbindung der beiden Punkte über h (Spiegel) ist. Analgog ist "Augen-A'" genau so lang wie "Augen-S1-Füße", also ebenfalls die kürzese Verbindung über den Spiegel. Anders formuliert muss der Spiegel die Strecke "S1-S2" abdecken.--CIG UA (Diskussion) 11:00, 14. Dez. 2018 (CET)
wie ist denn das Verhältnis vonzu
?--Schnirch (Diskussion) 13:08, 17. Dez. 2018 (CET)
|S1S2| ist halb so groß wie |A'B'|. Wenn wir einen Punkt X auf Höhe der Augen zwischen S1 und S2 anbringen, dann gilt: |XS2| ist halb so groß wie |XB'| und |XS1| ist halb so groß wie |XA'|, somit ist |S1S2| halb so groß wie |A'B'|.--CIG UA (Diskussion) 20:44, 20. Dez. 2018 (CET)