Lösung von Aufgabe 8.2P (WS 18 19)

Wie hoch muss ein Spiegel sein, damit Sie sich ganz darin sehen können und auf welcher Höhe muss die Oberkante des Spiegels angebracht werden? Anmerkung: Sie dürfen hier die Strahlensätze, wie sie aus der Schule bekannt sind, verwenden. Tipp: Hier finden Sie eine hilfreiche GeoGebra-Applikation.

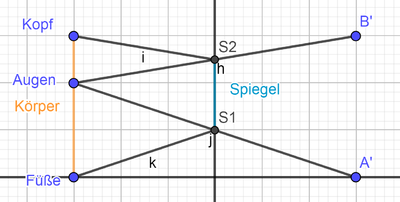
Der Spiegel muss so hoch hängen, dass er ab der Mitte der Strecke Füße-Augen anfängt, die Oberkante liegt bei der Mitte der Strecke Augen-Kopf (mit Kopf ist der oberste Teil des Kopfes gemeint).--CIG UA (Diskussion) 22:03, 6. Dez. 2018 (CET)

ok, die Zeichnung erklärt das Ganze schon sehr schön, können Sie das auch mathematisch formal korrekt begründen?--Schnirch (Diskussion) 11:55, 10. Dez. 2018 (CET)

Die Strecke "Augen-B'" ist genau so lang, wie "Augen-S2-Kopf", die somit auch kürzeste Verbindung der beiden Punkte über h (Spiegel) ist. Analgog ist "Augen-A'" genau so lang wie "Augen-S1-Füße", also ebenfalls die kürzese Verbindung über den Spiegel. Anders formuliert muss der Spiegel die Strecke "S1-S2" abdecken.--CIG UA (Diskussion) 11:00, 14. Dez. 2018 (CET)

wie ist denn das Verhältnis von $\left| S_1S_2 \right|$ zu $\left| A'B' \right|$?--Schnirch (Diskussion) 13:08, 17. Dez. 2018 (CET)

|S₁S₂| ist halb so groß wie |A'B'|. Wenn wir einen Punkt X auf Höhe der Augen zwischen S₁ und S₂ anbringen, dann gilt: |XS₂| ist halb so groß wie |XB'| und |XS¹| ist halb so groß wie |XA'|, somit ist |S₁S₂| halb so groß wie |A'B'|.--CIG UA (Diskussion) 20:44, 20. Dez. 2018 (CET)