Übungsaufgaben zur Algebra, Serie 2 SoSe 2019: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 01)
Zeile 7: Zeile 7:
 
=Aufgabe 02=
 
=Aufgabe 02=
 
Es sei <math>\mathbb{P}</math> die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ <math>y=mx</math> beschreibbar sind <math>(m\in \mathbb{R}, m \neq 0)</math>. Unter <math>\circ</math> wollen wir die NAF von Funktionen verstehen. Beweisen Sie: <math>[\mathbb{P}, \circ]</math> ist eine Untergruppe von <math>[\mathbb{L}, \circ]</math>.
 
Es sei <math>\mathbb{P}</math> die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ <math>y=mx</math> beschreibbar sind <math>(m\in \mathbb{R}, m \neq 0)</math>. Unter <math>\circ</math> wollen wir die NAF von Funktionen verstehen. Beweisen Sie: <math>[\mathbb{P}, \circ]</math> ist eine Untergruppe von <math>[\mathbb{L}, \circ]</math>.
 +
=Aufgabe 03=
 +
Untergruppenkriterium 1:<br />
 +
Es sei <math>[G, \circ]</math> eine Gruppe und <math>U \subseteq G</math>. <math>[U, \circ]</math> ist Untergruppe von <math>[G, \circ] \Leftrightarrow </math><br />
 +
# <math>\forall a, b \in U: a \circ b \in U</math>,
 +
# <math>\forall a \in U : a^{-1} \in U</math>.
 +
Beweisen Sie das Untergruppenkriterium 1
 +
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
|}
 
|}
 
</div>
 
</div>
 
[[Kategorie:Algebra]]
 
[[Kategorie:Algebra]]

Version vom 18. Juni 2019, 13:15 Uhr

Aufgabe 01

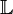Es sei \mathbb{L} die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 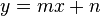y=mx+n beschreibbar sind 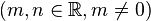(m,n\in \mathbb{R}, m \neq 0). Unter \circ wollen wir die NAF von Funktionen verstehen. Beweisen Sie: [\mathbb{L}, \circ] ist eine Gruppe.
Hinweis: Die NAF von Funktionen ist generell assoziativ. Diesbezüglich müssen Sie nichts beweisen.

Aufgabe 02

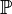Es sei \mathbb{P} die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 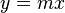y=mx beschreibbar sind 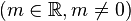(m\in \mathbb{R}, m \neq 0). Unter \circ wollen wir die NAF von Funktionen verstehen. Beweisen Sie: [\mathbb{P}, \circ] ist eine Untergruppe von [\mathbb{L}, \circ].

Aufgabe 03

Untergruppenkriterium 1:
Es sei [G, \circ] eine Gruppe und 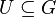U \subseteq G. [U, \circ] ist Untergruppe von [G, \circ] \Leftrightarrow

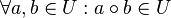  1. \forall a, b \in U: a \circ b \in U,
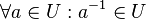  2. \forall a \in U : a^{-1} \in U.

Beweisen Sie das Untergruppenkriterium 1

Von „http://geometrie.zum.de/index.php?title=Übungsaufgaben_zur_Algebra,_Serie_2_SoSe_2019&oldid=33471“