Aufgabe 01
Es sei 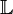 die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 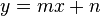 beschreibbar sind beschreibbar sind 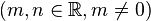 . Unter . Unter  wollen wir die NAF von Funktionen verstehen. Beweisen Sie: wollen wir die NAF von Funktionen verstehen. Beweisen Sie: ![[\mathbb{L}, \circ]](/images/math/5/b/a/5baaebd435ad00694430eefdeb350760.png) ist eine Gruppe. ist eine Gruppe.
Hinweis: Die NAF von Funktionen ist generell assoziativ. Diesbezüglich müssen Sie nichts beweisen.
Aufgabe 02
Es sei 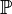 die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 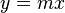 beschreibbar sind beschreibbar sind 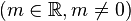 . Unter . Unter  wollen wir die NAF von Funktionen verstehen. Beweisen Sie: wollen wir die NAF von Funktionen verstehen. Beweisen Sie: ![[\mathbb{P}, \circ]](/images/math/5/5/4/554ca46f7c4c25b1c0181befce5d2bb6.png) ist eine Untergruppe von ist eine Untergruppe von ![[\mathbb{L}, \circ]](/images/math/5/b/a/5baaebd435ad00694430eefdeb350760.png) . .
Aufgabe 03
Untergruppenkriterium 1:
Es sei ![[G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe und eine Gruppe und 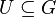 . . ![[U, \circ]](/images/math/b/e/9/be91aec2753430c87cc11578aed000df.png) ist Untergruppe von ist Untergruppe von ![[G, \circ] \Leftrightarrow](/images/math/0/f/d/0fd4c0a6b83b3400472ada8179f5f2b8.png)
-
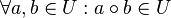 , ,
-
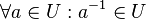 . .
Beweisen Sie das Untergruppenkriterium 1
Aufgabe 4
Unter der Kleinschen Vierergruppe versteht man eine Gruppe mit 4 Elementen, die alle selbstinvers sind.
Geben Sie 3 konkrete Kleinsche Viergruppen an, und betten Sie diese als ein Untergruppe in jeweils eine Obergruppe ein.
Aufgabe 5
Beweisen Sie: Wenn eine Gruppe die Ordnung 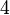 hat, dann ist sie entweder zyklisch oder sie ist eine Kleinsche Vierergruppe. hat, dann ist sie entweder zyklisch oder sie ist eine Kleinsche Vierergruppe.
Aufgabe 6
Wir definieren 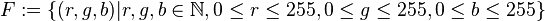 . Auf . Auf  legen wir eine Operation legen wir eine Operation  wie folgt fest: wie folgt fest: 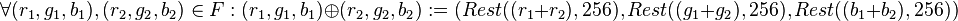 .
Beweisen Sie: .
Beweisen Sie: ![[F, \oplus]](/images/math/c/1/9/c19ff1a55e5e1b16b669d8b9e3c36ed3.png) ist eine Gruppe ist eine Gruppe
Aufgabe 7
Wir definieren 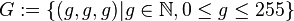 . Beweisen Sie: . Beweisen Sie: ![[G, \oplus]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) ist Untergruppe von ist Untergruppe von ![[F, \oplus]](/images/math/c/1/9/c19ff1a55e5e1b16b669d8b9e3c36ed3.png) . .
Aufgabe 8
Bestimmen Sie die Ordnungen der beiden Gruppen aus den Aufgaben 6 und 7. Erläutern Sie in diesem Zusammenhang den Satz von Lagrange.
Aufgabe 9
Geben Sie drei weitere Untergruppen von ![[F, \oplus]](/images/math/c/1/9/c19ff1a55e5e1b16b669d8b9e3c36ed3.png) an. an.
Aufgabe 10
Es sei  die Menge aller quadratischen Funktionen vom Typ die Menge aller quadratischen Funktionen vom Typ 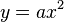 . Wir definieren für alle Funktionen dieses Typs eine Addition . Wir definieren für alle Funktionen dieses Typs eine Addition  wie folgt: wie folgt: 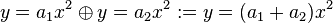 . Beweisen oder widerlegen Sie: . Beweisen oder widerlegen Sie:
![[Q, \oplus]](/images/math/a/b/c/abc09453ab3672e000dc93b6753eb0d7.png) ist eine Gruppe. ist eine Gruppe.
|  die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ
die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 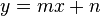 beschreibbar sind
beschreibbar sind 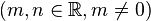 . Unter
. Unter  wollen wir die NAF von Funktionen verstehen. Beweisen Sie:
wollen wir die NAF von Funktionen verstehen. Beweisen Sie: ![[\mathbb{L}, \circ]](/images/math/5/b/a/5baaebd435ad00694430eefdeb350760.png) ist eine Gruppe.
ist eine Gruppe. 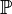 die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ
die Menge aller reellen Funktionen die durch eine Funktionsgleichung vom Typ 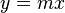 beschreibbar sind
beschreibbar sind 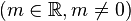 . Unter
. Unter ![[\mathbb{P}, \circ]](/images/math/5/5/4/554ca46f7c4c25b1c0181befce5d2bb6.png) ist eine Untergruppe von
ist eine Untergruppe von ![[G, \circ]](/images/math/4/6/8/4686bbf90bf7ebab892b288a31255920.png) eine Gruppe und
eine Gruppe und 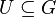 .
. ![[U, \circ]](/images/math/b/e/9/be91aec2753430c87cc11578aed000df.png) ist Untergruppe von
ist Untergruppe von ![[G, \circ] \Leftrightarrow](/images/math/0/f/d/0fd4c0a6b83b3400472ada8179f5f2b8.png)
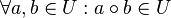 ,
,
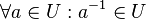 .
.
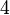 hat, dann ist sie entweder zyklisch oder sie ist eine Kleinsche Vierergruppe.
hat, dann ist sie entweder zyklisch oder sie ist eine Kleinsche Vierergruppe.
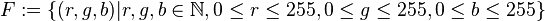 . Auf
. Auf  legen wir eine Operation
legen wir eine Operation  wie folgt fest:
wie folgt fest: 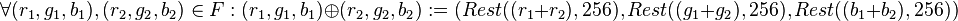 .
Beweisen Sie:
.
Beweisen Sie: ![[F, \oplus]](/images/math/c/1/9/c19ff1a55e5e1b16b669d8b9e3c36ed3.png) ist eine Gruppe
ist eine Gruppe
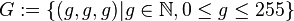 . Beweisen Sie:
. Beweisen Sie: ![[G, \oplus]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) ist Untergruppe von
ist Untergruppe von  die Menge aller quadratischen Funktionen vom Typ
die Menge aller quadratischen Funktionen vom Typ 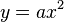 . Wir definieren für alle Funktionen dieses Typs eine Addition
. Wir definieren für alle Funktionen dieses Typs eine Addition 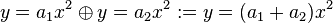 . Beweisen oder widerlegen Sie:
. Beweisen oder widerlegen Sie:![[Q, \oplus]](/images/math/a/b/c/abc09453ab3672e000dc93b6753eb0d7.png) ist eine Gruppe.
ist eine Gruppe.

