Sitzung 4 Drehungen Teil 1 2020: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Datei zum Experimentieren) |
||
| Zeile 11: | Zeile 11: | ||
==Datei zum Experimentieren== | ==Datei zum Experimentieren== | ||
| + | ===Aufgabe=== | ||
| + | ====didaktische Aufgabe==== | ||
| + | Generieren Sie Aufgaben für eine 7. Klasse im Kontext der folgenden Geogebraanwendung. | ||
| + | ====fachwissenschaftliche Aufgabe==== | ||
| + | Auch die unteren Eckpunkte jeder Gondel (<math>M_i, N_i</math> gehen durch jeweils eine Drehung ineinander über. | ||
| + | # Beschreiben Sie die Drehzentren dieser Drehungen. | ||
| + | # Beweisen Sie, dass es sich in diesen Fällen auch um Drehungen handelt. Sie dürfen davon ausgehen, dass die Aufhängungspunkte der Gondeln am Riesenrad durch Drehungen um <math>Z</math> ineinander übergehen.<br /> Vektorrechnung ist jetzt hilfreich. | ||
| + | |||
<iframe scrolling="no" title="Riesenrad" src="https://www.geogebra.org/material/iframe/id/dxxrsjkz/width/1268/height/799/border/888888/sfsb/true/smb/false/stb/true/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="1268px" height="799px" style="border:0px;"> </iframe> | <iframe scrolling="no" title="Riesenrad" src="https://www.geogebra.org/material/iframe/id/dxxrsjkz/width/1268/height/799/border/888888/sfsb/true/smb/false/stb/true/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="1268px" height="799px" style="border:0px;"> </iframe> | ||
[[Kategorie: Elementargeometrie]] | [[Kategorie: Elementargeometrie]] | ||
Version vom 20. Mai 2020, 14:58 Uhr
Inhaltsverzeichnis |
Das Whiteboard zur Sitzung
Original (interaktiv)
Whiteboard vom 19. Mai 2020 Elementargeometrie
PNG
SVG
Hinweis: Mittels der Freeware Inkscape können Sie das Format SVG schnell in PDF umwandeln, der Inhalt bleibt dabei Vektorgrafik.
Skript
In Arbeit
Datei zum Experimentieren
Aufgabe
didaktische Aufgabe
Generieren Sie Aufgaben für eine 7. Klasse im Kontext der folgenden Geogebraanwendung.
fachwissenschaftliche Aufgabe
Auch die unteren Eckpunkte jeder Gondel (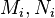 gehen durch jeweils eine Drehung ineinander über.
gehen durch jeweils eine Drehung ineinander über.
- Beschreiben Sie die Drehzentren dieser Drehungen.
- Beweisen Sie, dass es sich in diesen Fällen auch um Drehungen handelt. Sie dürfen davon ausgehen, dass die Aufhängungspunkte der Gondeln am Riesenrad durch Drehungen um
 ineinander übergehen.
ineinander übergehen.
Vektorrechnung ist jetzt hilfreich.
[ www.geogebra.org is not an authorized iframe site ]



