Sitzung 4 Drehungen Teil 1 2020: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Datei zum Experimentieren) |
*m.g.* (Diskussion | Beiträge) (→Skript) |
||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[https://wbd.ms/share/v2/aHR0cHM6Ly93aGl0ZWJvYXJkLm1pY3Jvc29mdC5jb20vYXBpL3YxLjAvd2hpdGVib2FyZHMvcmVkZWVtL2M0YjM5Zjc0YTcyMTQ5MDc5Yjg0NTU4Zjk0OTg5Yzk4X2EzNTcwOTZiLTE0YTMtNGQ4Ny1hMWMyLTQ3NWQ0ZDlmMzFkZg== Whiteboard vom 19. Mai 2020 Elementargeometrie] | [https://wbd.ms/share/v2/aHR0cHM6Ly93aGl0ZWJvYXJkLm1pY3Jvc29mdC5jb20vYXBpL3YxLjAvd2hpdGVib2FyZHMvcmVkZWVtL2M0YjM5Zjc0YTcyMTQ5MDc5Yjg0NTU4Zjk0OTg5Yzk4X2EzNTcwOTZiLTE0YTMtNGQ4Ny1hMWMyLTQ3NWQ0ZDlmMzFkZg== Whiteboard vom 19. Mai 2020 Elementargeometrie] | ||
==PNG== | ==PNG== | ||
| − | + | http://geometrie.zum.de/wiki/Datei:WBElementargeometrie19Mai2020PNG.png | |
| + | |||
==SVG== | ==SVG== | ||
Hinweis: Mittels der Freeware [https://inkscape.org/de/ Inkscape] können Sie das Format SVG schnell in PDF umwandeln, der Inhalt bleibt dabei Vektorgrafik.<br /> | Hinweis: Mittels der Freeware [https://inkscape.org/de/ Inkscape] können Sie das Format SVG schnell in PDF umwandeln, der Inhalt bleibt dabei Vektorgrafik.<br /> | ||
| − | + | http://geometrie.zum.de/wiki/Datei:WBElementargeometrie19Mai2020SVG.svg | |
| + | |||
==Skript== | ==Skript== | ||
| − | + | [[Datei:Drehung Elementargeometrie SoSe 2020.pdf|Drehungen in der Schule, als Bewegungen mit genau einem Fixpunkt und als NAF zweier GeradenspieglungenSkript zur Konferenz am 19. Mai 2020 Elementargeometrieund ein wenig mehr schon für die folgenden Sitzung]] | |
==Datei zum Experimentieren== | ==Datei zum Experimentieren== | ||
Für spätere Einsätze finden Sie die Datei auf meinem Geogebrakanal: [https://www.geogebra.org/m/ejvuz7fp Riesenrad]<br /> | Für spätere Einsätze finden Sie die Datei auf meinem Geogebrakanal: [https://www.geogebra.org/m/ejvuz7fp Riesenrad]<br /> | ||
| − | Als animated Gif: [[Bild:Riesenrad2.gif|200px]] | + | Als animated Gif: [[Bild:Riesenrad2.gif|200px]]<br /> |
| + | Stichwort Medienkompetenz: Was bedeutet GIF? Und nein, GIF steht nicht für Zappelbild aus dem Internet. Sie haben es mit dem ältesten Bildformat des internets zu tun. Ein Klassiker, der trotz seiner Beschränkheit nicht tot zu kriegen ist. | ||
===Aufgabe=== | ===Aufgabe=== | ||
====didaktische Aufgabe==== | ====didaktische Aufgabe==== | ||
| Zeile 23: | Zeile 26: | ||
<iframe scrolling="no" title="Riesenrad" src="https://www.geogebra.org/material/iframe/id/dxxrsjkz/width/1268/height/799/border/888888/sfsb/true/smb/false/stb/true/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="634px" height="400px" style="border:0px;"> </iframe> | <iframe scrolling="no" title="Riesenrad" src="https://www.geogebra.org/material/iframe/id/dxxrsjkz/width/1268/height/799/border/888888/sfsb/true/smb/false/stb/true/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="634px" height="400px" style="border:0px;"> </iframe> | ||
| + | |||
==Polarkoordinatensysteme zum Ausdrucken== | ==Polarkoordinatensysteme zum Ausdrucken== | ||
* SVG : [[Datei:Polarkoordinatensytem1.svg|Polarkoordinatesystem als SVG Datei]] | * SVG : [[Datei:Polarkoordinatensytem1.svg|Polarkoordinatesystem als SVG Datei]] | ||
* EPS : [[Datei:Polarkoordinatensytem.eps|Polarkoordinatensystem als gekapseltes Postscript EPS]] | * EPS : [[Datei:Polarkoordinatensytem.eps|Polarkoordinatensystem als gekapseltes Postscript EPS]] | ||
| + | ==Übungsaufgaben== | ||
| + | ===Aufgabe 5.1=== | ||
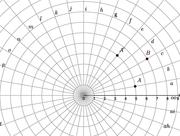
| + | [[Datei:Polarkoordinaten01-eps-converted-to.pdf|Punkte im Polarkoordinatensystem]]<br /> | ||
| + | # Der Punkt <math>A</math> liegt auf dem Strahl <math>a</math> und dem Kreis <math>5</math>. Sein Bild <math>A'</math> bei der Drehung um das Zentrum liegt auf dem Strahl <math>e</math> und dem Kreis <math>5</math> . Der Punkt B liegt auf dem Strahl <math>c</math> und dem Kreis <math>7</math>. Wo liegt sein Bild <math>B'</math>, wenn er derselben Drehung wie <math>A</math> unterworfen wird? | ||
| + | # Zeichne den Punkt <math>D</math> mit den Koordinaten <math>(3,c)</math> und sein Bild <math>D'</math> ein.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.) | ||
| + | # <math>D'</math> liegt bei <math>(w,4)</math>. Wo befindet sich seine zugehöriger Originalpunkt.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.) | ||
| + | [[Lösungen Aufgabe 5.1 Elementargeometrie SoSe 2020]] | ||
| + | |||
| + | ===Aufgabe 5.2=== | ||
| + | Sie haben vor, die Erarbeitung der Vorschrift zur Konstruktion des Bildes <math>P'</math> eines Punktes <math>P</math> bei einer Drehung um <math>Z</math> mit dem Drehwinkel <math>\alpha</math> und vorgegebnem Drehsinn mittels eines Polarkoordinatensystems zu unterstützen. Klassifizieren Sie diesbezüglich wenigstens vier verschiedene Aufgabentypen und formulieren Sie zu jedem ihrer Typen drei Beispielaufgaben für den Einsatz in einer 7. Klasse einer Werkrealschule. Fassen Sie Ihre Aufgaben auf einem Arbeitsblatt im Format PDF zusammen und veröffentlichen Sie Ihr Arbeitsblatt im Wiki.<br /> | ||
| + | Weitere Rahmenbedingung: Die Arbeitsblätter müssen Polarkoordinatensysteme enthalten. Reale Zeichnungen, die fotografiert wurden, sind nicht erlaubt. Alles rein digital. In die folgende Datei können Sie Ihre Arbeitsblätter integrieren:<br /> | ||
| + | |||
| + | [[Zu den Arbeitsblättern, Drehung mittels Polarkoordinaten SoSe2020]] | ||
| + | |||
[[Kategorie: Elementargeometrie]] | [[Kategorie: Elementargeometrie]] | ||
Aktuelle Version vom 21. Mai 2020, 17:05 Uhr
Inhaltsverzeichnis |
Das Whiteboard zur Sitzung
Original (interaktiv)
Whiteboard vom 19. Mai 2020 Elementargeometrie
PNG
http://geometrie.zum.de/wiki/Datei:WBElementargeometrie19Mai2020PNG.png
SVG
Hinweis: Mittels der Freeware Inkscape können Sie das Format SVG schnell in PDF umwandeln, der Inhalt bleibt dabei Vektorgrafik.
http://geometrie.zum.de/wiki/Datei:WBElementargeometrie19Mai2020SVG.svg
Skript
Datei zum Experimentieren
Für spätere Einsätze finden Sie die Datei auf meinem Geogebrakanal: Riesenrad
Als animated Gif: 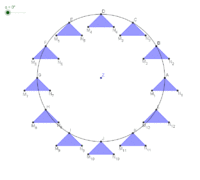
Stichwort Medienkompetenz: Was bedeutet GIF? Und nein, GIF steht nicht für Zappelbild aus dem Internet. Sie haben es mit dem ältesten Bildformat des internets zu tun. Ein Klassiker, der trotz seiner Beschränkheit nicht tot zu kriegen ist.
Aufgabe
didaktische Aufgabe
Generieren Sie Aufgaben für eine 7. Klasse im Kontext der folgenden Geogebraanwendung.
fachwissenschaftliche Aufgabe
Auch die unteren Eckpunkte jeder Gondel (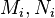 gehen durch jeweils eine Drehung ineinander über.
gehen durch jeweils eine Drehung ineinander über.
- Beschreiben Sie die Drehzentren dieser Drehungen.
- Beweisen Sie, dass es sich in diesen Fällen auch um Drehungen handelt. Sie dürfen davon ausgehen, dass die Aufhängungspunkte der Gondeln am Riesenrad durch Drehungen um
 ineinander übergehen.
ineinander übergehen.
Vektorrechnung ist jetzt hilfreich.
[ www.geogebra.org is not an authorized iframe site ]
Polarkoordinatensysteme zum Ausdrucken
- SVG :

- EPS : Datei:Polarkoordinatensytem.eps
Übungsaufgaben
Aufgabe 5.1
- Der Punkt
 liegt auf dem Strahl
liegt auf dem Strahl  und dem Kreis
und dem Kreis 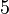 . Sein Bild
. Sein Bild 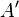 bei der Drehung um das Zentrum liegt auf dem Strahl
bei der Drehung um das Zentrum liegt auf dem Strahl  und dem Kreis
und dem Kreis 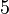 . Der Punkt B liegt auf dem Strahl
. Der Punkt B liegt auf dem Strahl  und dem Kreis
und dem Kreis 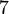 . Wo liegt sein Bild
. Wo liegt sein Bild 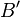 , wenn er derselben Drehung wie
, wenn er derselben Drehung wie  unterworfen wird?
unterworfen wird?
- Zeichne den Punkt
 mit den Koordinaten
mit den Koordinaten 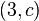 und sein Bild
und sein Bild 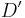 ein.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.)
ein.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.)
-
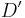 liegt bei
liegt bei 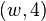 . Wo befindet sich seine zugehöriger Originalpunkt.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.)
. Wo befindet sich seine zugehöriger Originalpunkt.(Wir gehen von derselben Drehung wie bei Aufgabe a) aus.)
Lösungen Aufgabe 5.1 Elementargeometrie SoSe 2020
Aufgabe 5.2
Sie haben vor, die Erarbeitung der Vorschrift zur Konstruktion des Bildes 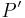 eines Punktes
eines Punktes  bei einer Drehung um
bei einer Drehung um  mit dem Drehwinkel
mit dem Drehwinkel  und vorgegebnem Drehsinn mittels eines Polarkoordinatensystems zu unterstützen. Klassifizieren Sie diesbezüglich wenigstens vier verschiedene Aufgabentypen und formulieren Sie zu jedem ihrer Typen drei Beispielaufgaben für den Einsatz in einer 7. Klasse einer Werkrealschule. Fassen Sie Ihre Aufgaben auf einem Arbeitsblatt im Format PDF zusammen und veröffentlichen Sie Ihr Arbeitsblatt im Wiki.
und vorgegebnem Drehsinn mittels eines Polarkoordinatensystems zu unterstützen. Klassifizieren Sie diesbezüglich wenigstens vier verschiedene Aufgabentypen und formulieren Sie zu jedem ihrer Typen drei Beispielaufgaben für den Einsatz in einer 7. Klasse einer Werkrealschule. Fassen Sie Ihre Aufgaben auf einem Arbeitsblatt im Format PDF zusammen und veröffentlichen Sie Ihr Arbeitsblatt im Wiki.
Weitere Rahmenbedingung: Die Arbeitsblätter müssen Polarkoordinatensysteme enthalten. Reale Zeichnungen, die fotografiert wurden, sind nicht erlaubt. Alles rein digital. In die folgende Datei können Sie Ihre Arbeitsblätter integrieren:
Zu den Arbeitsblättern, Drehung mittels Polarkoordinaten SoSe2020