Der Zentriwinkel-Peripheriewinkelsatz: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Der Zentrie-Peripheriewinkelsatz) |
|||
| Zeile 5: | Zeile 5: | ||
{{#ev:youtube|QyCtXT3mGjI}} | {{#ev:youtube|QyCtXT3mGjI}} | ||
| − | == Der | + | == Der Zentri-Peripheriewinkelsatz == |
| − | ===Definition ( | + | ===Definition (Zentriwinkel, Mittelpunktswinkel)=== |
| − | Ist M der Mittelpunkt des Kreises k, so bezeichnet man einen Winkel <math> \angle AMB </math> als den zughörigen | + | Ist M der Mittelpunkt des Kreises k, so bezeichnet man einen Winkel <math> \angle AMB </math> als den zughörigen Zentriwinkel (Mittelpunktswinkel). |
| − | === Satz:(Der | + | === Satz:(Der Zentri-Peripheriewinkelsatz) === |
Jeder Peripheriewinkel ist halb so groß, wie ein zugehöriger Zentriwinkel. | Jeder Peripheriewinkel ist halb so groß, wie ein zugehöriger Zentriwinkel. | ||
Version vom 23. Juli 2010, 17:51 Uhr
Inhaltsverzeichnis[Verbergen] |
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
Der Zentri-Peripheriewinkelsatz
Definition (Zentriwinkel, Mittelpunktswinkel)
Ist M der Mittelpunkt des Kreises k, so bezeichnet man einen Winkel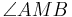 
als den zughörigen Zentriwinkel (Mittelpunktswinkel).
Satz:(Der Zentri-Peripheriewinkelsatz)
Jeder Peripheriewinkel ist halb so groß, wie ein zugehöriger Zentriwinkel.
