Der Zentriwinkel-Peripheriewinkelsatz
Inhaltsverzeichnis |
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
Der Zentri-Peripheriewinkelsatz
Definition (Zentriwinkel, Mittelpunktswinkel)
Ist M der Mittelpunkt des Kreises k, so bezeichnet man einen Winkel 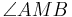 als den zughörigen Zentriwinkel (Mittelpunktswinkel).
als den zughörigen Zentriwinkel (Mittelpunktswinkel).
Definition (Peripheriewinkel)
Sei k ein Kreis und alpha ein Winkel. Alpha ist Peripheriewinkel von k, wenn sein Scheitelpunkt auf dem Kreis k liegt und seine beiden Schenkeln den Kreis k in jeweils einem weiteren Punkt schneiden.
Satz:(Der Zentri-Peripheriewinkelsatz)
(abgeändert) Jeder Peripheriewinkel ist halb so groß, wie sein zugehöriger Zentriwinkel.
Kommentar --*m.g.* 20:59, 23. Jul. 2010 (UTC): Vorsicht mit den Artikeln: Wie viele Zentriwinkel sind einem Peripheriewinkel zugehörig? In der Definition war es korrekt.
Beweis
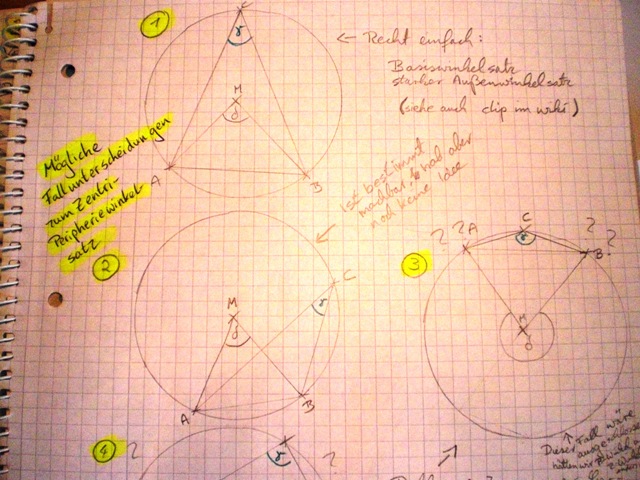
Ich hab mir Gedanken zu den Fallunterscheidungen gemacht, komme aber irgendwie nicht weiter. Ich stelle meine Notizen mal hier ein, kann mir jemand weiter helfen?
--Barbarossa 13:22, 25. Jul. 2010 (UTC)
Jaaaaaaaaa :-) Ich glaube, ich hatte gerade DIE Eingebung, zumindest bezüglich der Fallunterscheidungen ;-).
Und zwar:
Laut dem Peripheriewinkelsatz sind alle Peripheriewinkel eines Kreises über einer Sehne gleich groß. Ich kann also sagen, dass ich den Scheitelpunkt des Peripheriewinkels so wähle, dass er auf der Mittelsenkrechten der Sehne liegt. Damit würden zumindest die Fälle 2 und 5 wegfallen.
Hm, naja, ob es allerdings viel hilft? Denn schließlich wären ja gerade Fall 3 und 4 die "unmöglichen Beweise"... Egal, Hauptsache Eingebung :-)
--Barbarossa 12:45, 26. Jul. 2010 (UTC)
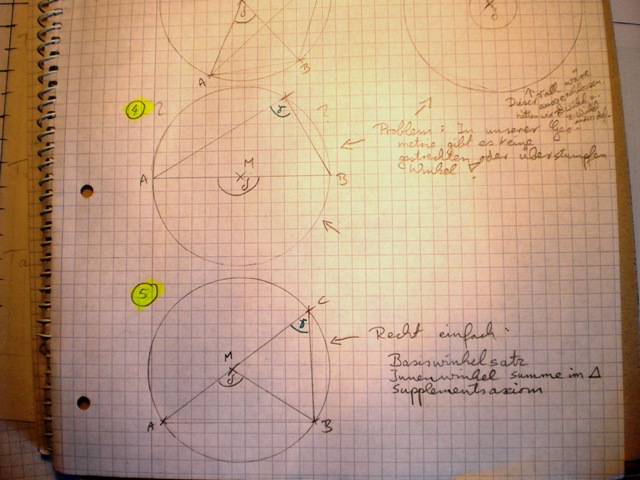
Überlegung--Löwenzahn 16:02, 26. Jul. 2010 (UTC)
- Könnte ich nicht Fall 1 so umändern, dass Fall 5 daraus wird: Wegen dem Satz "Peripheriewinkel über ein und derselben Sehne sind kongruent zueinander". Dann könnte man wie bei Fall 5 weiter argumentieren und man hätte auch schon Fall 2 drin.
- Fall 3 und 4 sind nicht beweisbar, wegen unserem Winkelmaß zwischen 0 und 180.
- zu Fall 2: könnte man nicht hier auch wieder eine Strecke
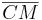 konstruieren, wodurch wieder eine ähnliche Beweisführung wie bei Fall 1 eintritt?
konstruieren, wodurch wieder eine ähnliche Beweisführung wie bei Fall 1 eintritt?
Mal so ne blöde Frage zwischendurch: Haben wir schon bewiesen, dass der Radius immer gleich groß bleibt!?
Ich glaub wir haben den Radius schon indirekt durch unsere Definition des Kreises festgelegt. Es kann keinen Punkt eines Kreises k geben der einen anderen Abstand zum Mittelpunkt von k hat als der Rest der Punkte von k (nach Def. Kreis), denn sonst wäre es kein Kreis mehr... --Principella 19:40, 26. Jul. 2010 (UTC)
OK, ich bin soweit durch mit meinem Beweis - fängt an mit Basiswinkelsätzen, dem starken Außenwinkelsatz und dem Winkeladditionsaxiom zum Schluss... Aber wie kann man jetzt zahlenmäßig beweisen, dass der Zentriewinkel doppelt so groß ist, wie der zugehörige Peripheriewinkel!??--TimoRR 13:41, 27. Jul. 2010 (UTC)
Ich gehe mal davon aus, dass du gezeigt hast, dass  und sein Basiswinkel, ich nenne ihn mal
und sein Basiswinkel, ich nenne ihn mal 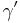 kongruent sind. Dann weiß du nach dem starken Außenwinkelsatz dass
kongruent sind. Dann weiß du nach dem starken Außenwinkelsatz dass 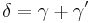 gilt. Da jetzt
gilt. Da jetzt 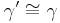 gilt, folgt
gilt, folgt 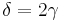 .--Löwenzahn 15:43, 27. Jul. 2010 (UTC)
.--Löwenzahn 15:43, 27. Jul. 2010 (UTC)
Alles klar, bin etwas durcheinandergekommen, weil ich die Winkelbezeichnungen, <ABM z.B. benutze und nicht alpha und beta... Kann ich dann einfach bei der Klausur die Winkel in meiner Skizze benennen und mich dann auf die Skizze berufen oder ab wann sollte man sich für alpha und beta bzw. <AMP und so weiter entscheiden!? --TimoRR 07:57, 28. Jul. 2010 (UTC)
Gestern hat Herr Schnirch bestätigt, dass man sich auf eine Skizze beziehen kann. Und dann würde ich auch mit alpha, beta weiterarbeiten. Zum einen weniger zum schreiben und zum anderen einfach übersichtlicher/leichter nachvollziehbar. --Löwenzahn 10:31, 28. Jul. 2010 (UTC)
Beweisidee zu Fall 2 (Skizze):
Du benennst den Schnittpkt von den Strecken MB und AC, sagen wir P ist der Schnittpkt.
Der Winkel APB ist Außenwinkel von den Dreiecken APM und PBC. Mit dem starken Außenwinkelsatz bekommst du 2 Gleichungen für den Winkel APB, die du gleichsetzen kannst...
Tipp: Du brauchst die kongruenten Winkel des gleichschenkligen Dreiecks AMC
Sorry wegen meinem Schreibstil :)--Principella 23:58, 28. Jul. 2010 (UTC)