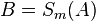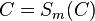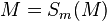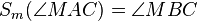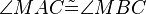Der Basiswinkelsatz WS 22 23: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Satz VIII.1: (Basiswinkelsatz)) |
(→Satz VIII.1: (Basiswinkelsatz)) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 39: | Zeile 39: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>C=S_{m}(C)</math> | | <math>C=S_{m}(C)</math> | ||
| − | | | + | | 2); C ist Fixpunkt (Def. Geradenspiegelung) |
| | | | ||
|- | |- | ||
| Zeile 45: | Zeile 45: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>M=S_{m}(M)</math> | | <math>M=S_{m}(M)</math> | ||
| − | | | + | | 2); M ist Fixpunkt (Def. Geradenspiegelung) |
| | | | ||
|- | |- | ||
| Zeile 51: | Zeile 51: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math> S_{m} (\angle MAC ) = \angle MBC </math> | | <math> S_{m} (\angle MAC ) = \angle MBC </math> | ||
| − | | | + | | 3); 4); 5); Winkeltreue der Geradenspiegelung |
| | | | ||
|- | |- | ||
| Zeile 58: | Zeile 58: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>\angle MAC \tilde {=} \angle MBC </math> | | <math>\angle MAC \tilde {=} \angle MBC </math> | ||
| − | | | + | | 6a); Winkelmaßerhaltung der Geradenspiegelung |
| | | | ||
|- | |- | ||
Aktuelle Version vom 5. Dezember 2022, 14:45 Uhr
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Ein Dreieck mit zwei zueinander kongruenten Seiten heißt gleichschenkliges Dreieck. Die beiden zueinander kongruenten Seiten heißen Schenkel, die dritte Seite heißt Basis des Dreiecks und die Innenwinkel an der Basis heißen Basiswinkel.
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Dreieck ist gleichschenklig
Behauptung: Basiswinkel sind kongruent
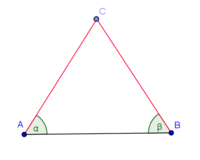
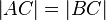
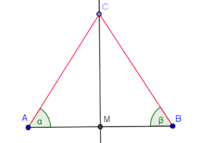
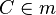 mit
mit  ist Mittelsenkrechte von
ist Mittelsenkrechte von