Arbeitsblätter Matheförderung: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Arbeitsblatt 01) |
*m.g.* (Diskussion | Beiträge) (→Potenzen und Potenzgesetze) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:Arbeitsblatt Mathe Foerderunterricht 01.pdf|Serie01]] | [[Datei:Arbeitsblatt Mathe Foerderunterricht 01.pdf|Serie01]] | ||
==Arbeitsblatt 02== | ==Arbeitsblatt 02== | ||
| + | ===Potenzen und Potenzgesetze=== | ||
| + | [[Datei:AB 02 qr.pdf|qr code]] | ||
| + | [[Datei:Arbeitsblatt Mathe Foerderunterricht 02.pdf|Potenzen und Potenzgesetze]] | ||
| + | |||
| + | ==Arbeitsblatt 03== | ||
| + | (wird in Kürze ergänzt hier als PDF erscheinen. | ||
===Lineare Funktionen=== | ===Lineare Funktionen=== | ||
====Aufgabe 1==== | ====Aufgabe 1==== | ||
| Zeile 11: | Zeile 17: | ||
====Aufgabe 3==== | ====Aufgabe 3==== | ||
Zeichne den Funktionsgraphen der proportionalen Funktion <math>y=\frac{3}{4}x</math>. Zeichne dann eine Gerade die im Koordinatenursprung senkrecht auf dem bereits gezeichneten Graphen steht. Bestimme die Funktionsgleichung für diese senkrechte Gerade. Vergleiche die Anstiege der beiden Geraden. | Zeichne den Funktionsgraphen der proportionalen Funktion <math>y=\frac{3}{4}x</math>. Zeichne dann eine Gerade die im Koordinatenursprung senkrecht auf dem bereits gezeichneten Graphen steht. Bestimme die Funktionsgleichung für diese senkrechte Gerade. Vergleiche die Anstiege der beiden Geraden. | ||
| − | ====Aufgabe 4 | + | ====Aufgabe 4==== |
Gegeben seien die beiden Punkte <math>A(-2|3)</math> und <math>B(-1|-2)</math>. Bestimme die die Funktionsgleichung für die Gerade, die durch beide Punkte geht. Bestimme dann die Funktionsgleichung für die Mittelsenkrechte der Strecke <math>\overline{AB}</math> | Gegeben seien die beiden Punkte <math>A(-2|3)</math> und <math>B(-1|-2)</math>. Bestimme die die Funktionsgleichung für die Gerade, die durch beide Punkte geht. Bestimme dann die Funktionsgleichung für die Mittelsenkrechte der Strecke <math>\overline{AB}</math> | ||
| + | |||
====Aufgabe 5==== | ====Aufgabe 5==== | ||
Der Mittelpunkt des Kreises k sei der Koordinatenursprung. k sei ein Einheitskreis, d.h. sei Radius hat die Länge 1. Bestimme die Koordinaten der beiden Schnittpunkte, die die Gerade <math>y=x</math> mit <math>k</math> hat. Bestimme die Gleichungen der Tangenten an <math>k</math> in diesen beiden Punkten. | Der Mittelpunkt des Kreises k sei der Koordinatenursprung. k sei ein Einheitskreis, d.h. sei Radius hat die Länge 1. Bestimme die Koordinaten der beiden Schnittpunkte, die die Gerade <math>y=x</math> mit <math>k</math> hat. Bestimme die Gleichungen der Tangenten an <math>k</math> in diesen beiden Punkten. | ||
Aktuelle Version vom 29. November 2023, 11:26 Uhr
Inhaltsverzeichnis |
Matheförderung
Arbeitsblatt 01
Deutsch-Mathe/Mathe-Deutsch
Arbeitsblatt 02
Potenzen und Potenzgesetze
Arbeitsblatt 03
(wird in Kürze ergänzt hier als PDF erscheinen.
Lineare Funktionen
Aufgabe 1
Gegeben seien die beiden Punkte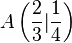 
und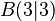 
. Der Funktionsgraph der Funktion 
sei die Gerade 
. Gib eine Funktionsgleichung von f an.
Aufgabe 2
Gegeben sei die lineare Gleichung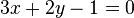 
. Forme diese Gleichung zu einer Funktionsgleichung vom Typ 
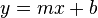um und zeichne den Graphen dieser Funktion.
Aufgabe 3
Zeichne den Funktionsgraphen der proportionalen Funktion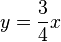 
. Zeichne dann eine Gerade die im Koordinatenursprung senkrecht auf dem bereits gezeichneten Graphen steht. Bestimme die Funktionsgleichung für diese senkrechte Gerade. Vergleiche die Anstiege der beiden Geraden.
Aufgabe 4
Gegeben seien die beiden Punkte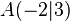 
und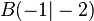 
. Bestimme die die Funktionsgleichung für die Gerade, die durch beide Punkte geht. Bestimme dann die Funktionsgleichung für die Mittelsenkrechte der Strecke 
Aufgabe 5
Der Mittelpunkt des Kreises k sei der Koordinatenursprung. k sei ein Einheitskreis, d.h. sei Radius hat die Länge 1. Bestimme die Koordinaten der beiden Schnittpunkte, die die Gerade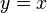 
mit 
hat. Bestimme die Gleichungen der Tangenten an in diesen beiden Punkten.
