Lösung von Aufgabe 1.2 WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
Tja??? (Diskussion | Beiträge) |
||
| Zeile 14: | Zeile 14: | ||
Den Rest können Sie alleine ... . | Den Rest können Sie alleine ... . | ||
| + | |||
| + | ===Lösungsmöglichkeit 1=== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |<u>Voraussetzung:</u>|| Existenz von A, B, C mit A ungleich B, B ungleich C , C ungleich A und Zw (A, B, C) | ||
| + | |- | ||
| + | |<u>Behauptung:</u>|| <math>\ |A'B'| + |B'C'| = |A'C'|</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="wikitable center" | ||
| + | |- style="background: #DDFFDD;" | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | | (I) | ||
| + | | <math>\ |AB| + |BC| = |AC|</math> | ||
| + | | Voraussetzung + Def. Zwischenrelation | ||
| + | |- | ||
| + | | (II) | ||
| + | | <math>\ |AB| = |A'B'|; |BC| = |B'C'|;|AC| = |A'C'|</math> | ||
| + | | (I) + Abstandsinvarianz der Bewegung (Def. Bewegung) | ||
| + | |- | ||
| + | | (III) | ||
| + | | <math>\ |A'B'| + |B'C'| = |A'C'|</math> | ||
| + | | (I)+(II) Rechnen mit rationalen Zahlen | ||
| + | |- | ||
| + | | (IV) | ||
| + | | <math>\operatorname{Zw}(A', B', C')</math> | ||
| + | | (III) + Def. Zwischenrelation | ||
| + | |}--[[Benutzer:Tja???|Tja???]] 17:56, 19. Okt. 2010 (UTC) | ||
Version vom 19. Oktober 2010, 18:56 Uhr
Es seien  drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
(*) 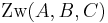 .
.
zu zeigen:
(**) 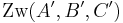
Wir übersetzen zunächst (*):
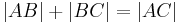
entsprechend (**) haben wir zu zeigen, dass 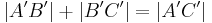 gilt.
gilt.
Den Rest können Sie alleine ... .
Lösungsmöglichkeit 1
| Voraussetzung: | Existenz von A, B, C mit A ungleich B, B ungleich C , C ungleich A und Zw (A, B, C) |
| Behauptung: | 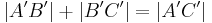
|
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 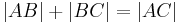
|
Voraussetzung + Def. Zwischenrelation |
| (II) | 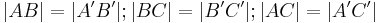
|
(I) + Abstandsinvarianz der Bewegung (Def. Bewegung) |
| (III) | 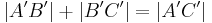
|
(I)+(II) Rechnen mit rationalen Zahlen |
| (IV) | 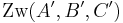
|
(III) + Def. Zwischenrelation |

