Benutzer:Tja???
Inhaltsverzeichnis |
Nacheinanderausführung von Bewegungen
|
Geradenspiegelung 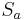
|
Drehung 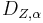
|
Verschiebung 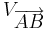
|
Schubspiegelung 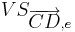
|
|---|---|---|---|---|
Geradenspiegelung 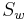
|
Verschiebung ( 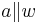 ) , ) ,Id. (a = w), Drehung |
Geradenspiegelung ( 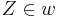 ), ), Schubspiegelung ( 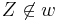 ) )
|
Geradenspiegelung ( 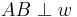 ), ), Schubspiegelung (sonst) |
Verschiebung ( 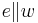 ), ), Drehung (sonst) [Punktspiegelung ( 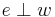 )] )]
|
Drehung 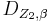
|
analog | Verschiebung (  °) °)Drehung (sonst) |
Verschiebung ( 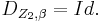 ), ),Drehung |
Geradenspiegelung ( 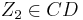 ) oder anderer Spezialfall), ) oder anderer Spezialfall),Schubspiegelung (sonst) |
Verschiebung 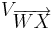
|
analog | analog | Verschiebung ( 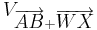 ) )
|
Geradenspiegelung ( 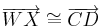 ), ),Schubspiegelung (sonst) |
Schubspiegelung 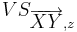
|
analog | analog | analog | Verschiebung ( 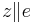 ), ), Drehung (sonst) |
Das ist nur eine Überlegung und bestimmt nicht komplett. Wenn jemand die Literatur von Herrn Schupf hat, bitte kontrollieren. Oder auch sonst Meinungen dazuschreiben!
Aufgabe zu gleichseitigen Dreiecken von Studenten
Aufgabe 1:
Man falte folgendermaßen aus einem DinA4 Blatt ein gleichseitiges Dreieck:
a) Man gehe folgendermaßen vor, um aus einem DinA4 Blatt ein gleichseitiges Dreieck zu erhalten. Man falte das Blatt so zusammen, dass die länger Seite auf die andere längere Seite fällt. Man öffnet das Papier wieder und klappt die Ecke D so ein, dass die Faltlinie n direkt in der Ecke A beginnt und D auf der zuvor entstandenen Faltlinie k liegt. Dann klappt man den restlichen Teil des Blattes über die neu Seite FE (siehe Skizze). Die überstehende Ecke B muss man jetzt noch nach hinten umklappen. Das Dreick AFG ist gleichschenklig.
Beweise dir Korrektheit dieser Handlung.
Lösungshinweise
b) Lässt sich dies auch mit einem quadratischen Papier oder mit einem Rechteck der Breite a und Länge 2a durchführen? Begründe.
c) Kann man auf diese Weiße auch ein Tetraeder herstellen?
Alte Prüfungsaufgaben
Segmentprüfung SS2008
Thema I A a)
Gegeben seien ein Winkel mit dem Scheitel S und den Schenkeln p, q so wie ein Punkt A im Inneren des Winkels.
Konstruieren Sie eine Gerade, die p in P und q in Q schneidet, so dass 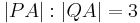 gilt.
Konstruktionund Konstruktionsbeschreibung
gilt.
Konstruktionund Konstruktionsbeschreibung
Thema I A b)
Beweisen Sie: Die Nacheinanderführung zweier zentrischer Streckungen mit den Streckfaktoren k und k2 ist für k*k2 = 1 eine Verschiebung.
Thema I A c)
Thema II c)
Konstruktion eines Dreiecks mit 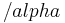 = 60°, b/c = 2/3 und Umkreisradius r= 4,5 cm
= 60°, b/c = 2/3 und Umkreisradius r= 4,5 cm
Thema II d)
Konstruktion+Konstruktionsvorschrift für Strecke x = (a²+b²)/f

