Fixpunkt, Fixgerade, Fixpunktgerade (2010): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Tja??? (Diskussion | Beiträge) (→Definition) |
Tja??? (Diskussion | Beiträge) (→Richtig verstanden?) |
||
| Zeile 53: | Zeile 53: | ||
=== Richtig verstanden? === | === Richtig verstanden? === | ||
| + | <quiz display="simple"> | ||
| + | {Kennzeichnen Sie die wahren Aussagen} | ||
| + | + (a) Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung. | ||
| + | + (b) Jede Fixpunktgerade einer Abbildung ist eine Fixgerade dieser Abbildung. | ||
| + | |||
| + | - (c) Jede Fixgerade einer Abbildung ist eine Fixpunktgerade dieser Abbildung. | ||
| + | |||
| + | + (d) g sei Fixgerade der Bewegung <math>\phi</math>, dann gilt: <math>\forall P \in g . P = \phi (P)</math> --~~~~ | ||
| + | - (e) weitere Beispiele ... . | ||
| + | |||
| + | |||
| + | </quiz> | ||
Version vom 2. November 2010, 17:22 Uhr
Inhaltsverzeichnis |
Fixpunkte
Beispiele/Gegenbeispiele
Definition des Begriffs Fixpunkt einer Abbildung
Definition 3.1: (Fixpunkt einer Abbildung  )
)
- Ein Punkt
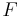 heißt Fixpunkt einer Abbildung
heißt Fixpunkt einer Abbildung  , wenn ... .
, wenn ... .
- Eine Abbildung
 heißt fixpunktfrei, wenn ... .
heißt fixpunktfrei, wenn ... .
- Ein Punkt
Richtig verstanden?
Fixgeraden
Beispiele/Gegenbeispiele
Definition
- Eine Gerade g, die bei der Abbildung
 auf sich selbst abgebildet wird, heißt Fixgerade g der Abbildung
auf sich selbst abgebildet wird, heißt Fixgerade g der Abbildung  . --Tja??? 16:08, 2. Nov. 2010 (UTC)
. --Tja??? 16:08, 2. Nov. 2010 (UTC)
- ...
Richtig verstanden?
Fixpunktgeraden
Beispiele/Gegenbeispiele
Definition
- Eine Fixgerade f einer Abbildung
 , bei der (mindestens) zwei Punkt der Fixgeraden f bei der Abbildung
, bei der (mindestens) zwei Punkt der Fixgeraden f bei der Abbildung  auf sich selbst abgebildet werden, heißt Fixpunktgerade. --Tja??? 16:06, 2. Nov. 2010 (UTC)
auf sich selbst abgebildet werden, heißt Fixpunktgerade. --Tja??? 16:06, 2. Nov. 2010 (UTC)
- ...

