Fixpunkt, Fixgerade, Fixpunktgerade (2010): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Richtig verstanden?)
(→‎Richtig verstanden?)
Zeile 68: Zeile 68:
  
 
Wenn die Aussage (a) heißt "Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung.", dann impliziert das ja, dass es Fixpunktgeraden gibt, die nicht zugleich Fixgeraden sind. Jede Fixpunktgerade einer Abbildung ist aber zugleich Fixgerade. Daher müsste die Aussage falsch sein.
 
Wenn die Aussage (a) heißt "Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung.", dann impliziert das ja, dass es Fixpunktgeraden gibt, die nicht zugleich Fixgeraden sind. Jede Fixpunktgerade einer Abbildung ist aber zugleich Fixgerade. Daher müsste die Aussage falsch sein.
 +
 +
Ich denke, dass "manche" genauso wie "eine" nicht ausschließt, dass dies für mehrere bzw. alle Fixpunktgeraden gilt!
  
 
Bei Aufgabe (d) wäre die Aussage nur richtig, wenn statt "Fixgerade" "FIxpunktgerade" stehen würde. Bei einer Fixgerade wird nur die Gerade auf sich selbst abgebildet, aber nicht unbedingt jeder Punkt der Geraden.
 
Bei Aufgabe (d) wäre die Aussage nur richtig, wenn statt "Fixgerade" "FIxpunktgerade" stehen würde. Bei einer Fixgerade wird nur die Gerade auf sich selbst abgebildet, aber nicht unbedingt jeder Punkt der Geraden.
 
--Steph85
 
--Steph85

Version vom 3. November 2010, 21:35 Uhr

Inhaltsverzeichnis

Fixpunkte

Beispiele/Gegenbeispiele

1. In welchen Fällen handelt es sich um Fixpunkte bezüglich der genannten Abbildung?

(a) Punkt \ A auf der Geraden \ g bezüglich der Spiegelung an \ g.
(b) Punkt \ A auf der Geraden \ g bezüglich einer Verschiebung längs \ g.
(c) Punkt \ Z bezüglich einer Drehung mit dem Drehwinkel \alpha = 30^\circ um \ Z.
(d) Punkt \ Z bezüglich einer Drehung mit dem Drehwinkel \alpha = 360^\circ um \ Z.
(e) Punkt A \notin g bezüglich der Spiegelung an \ g.
(f) Jeder Punkt \ Q bezüglich der Identität.
(g) Jeder Punkt \ D bezüglich einer zentrischen Streckung an dem Punkt \ Z.
(h) Der Punkt \ D bezüglich einer zentrischen Streckung an sich selbst.
(i) Jeder Punkt der Ebene \ \delta bezüglich einer senkrechten Parallelprojektion auf die Ebene \ \delta.
(j) Der Zentralpunkt \ Z einer Zentralprojektion.

Punkte: 0 / 0


Definition des Begriffs Fixpunkt einer Abbildung

Definition 3.1: (Fixpunkt einer Abbildung \ \phi )
Ein Punkt 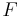\ F heißt Fixpunkt einer Abbildung \ \phi, wenn ... .
Eine Abbildung \ \phi heißt fixpunktfrei, wenn ... .

Richtig verstanden?

1. Kennzeichnen Sie die wahren Aussagen

(a) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_h.
(b) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_g.
(c) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_h \circ S_g.
(d) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_g \circ S_h.
(e) Jede Drehung hat genau einen Fixpunkt.
(f) Es gibt fixpunktfreie Geradenspiegelungen.
(g) Es gibt fixpunktfreie Verschiebungen.
(h) Ihr Beispiel ... .

Punkte: 0 / 0


Fixgeraden

Beispiele/Gegenbeispiele

Definition

  • Eine Gerade g, die bei der Abbildung \phi auf sich selbst abgebildet wird, heißt Fixgerade g der Abbildung \phi. --Tja??? 16:08, 2. Nov. 2010 (UTC)
  • Es seien g eine Gerade und \phi eine Abbildung. g ist genau dann eine Fixgerade bezüglich \phi, wenn jeder Punkt von g bei der Abbildung \phi wieder auf einen Punkt von g abgebildet wird. --Schomuf 08:32, 3. Nov. 2010 (UTC)
  • ...

Richtig verstanden?

Fixpunktgeraden

Beispiele/Gegenbeispiele

Definition

  • Eine Fixgerade f einer Abbildung \phi, bei der (mindestens) zwei Punkt der Fixgeraden f bei der Abbildung \phi auf sich selbst abgebildet werden, heißt Fixpunktgerade. --Tja??? 16:06, 2. Nov. 2010 (UTC)
  • ...

Richtig verstanden?

1. Kennzeichnen Sie die wahren Aussagen

(a) Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung.
(b) Jede Fixpunktgerade einer Abbildung ist eine Fixgerade dieser Abbildung.
(c) Jede Fixgerade einer Abbildung ist eine Fixpunktgerade dieser Abbildung.
(d) g sei Fixgerade der Bewegung \phi, dann gilt: \forall P \in g . P = \phi (P) --~~~~
(e) weitere Beispiele ... .

Punkte: 0 / 0

Ich glaube die Auflösungen von Aufgabe (a) und (d) sind nicht korrekt.

Wenn die Aussage (a) heißt "Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung.", dann impliziert das ja, dass es Fixpunktgeraden gibt, die nicht zugleich Fixgeraden sind. Jede Fixpunktgerade einer Abbildung ist aber zugleich Fixgerade. Daher müsste die Aussage falsch sein.

Ich denke, dass "manche" genauso wie "eine" nicht ausschließt, dass dies für mehrere bzw. alle Fixpunktgeraden gilt!

Bei Aufgabe (d) wäre die Aussage nur richtig, wenn statt "Fixgerade" "FIxpunktgerade" stehen würde. Bei einer Fixgerade wird nur die Gerade auf sich selbst abgebildet, aber nicht unbedingt jeder Punkt der Geraden. --Steph85

Von „http://geometrie.zum.de/index.php?title=Fixpunkt,_Fixgerade,_Fixpunktgerade_(2010)&oldid=4556“