Lösung von Aufgabe 1.3 WS2010): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Tja??? (Diskussion | Beiträge) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
<math>\beta_2 \circ \beta_1</math> ist eine Bewegung. | <math>\beta_2 \circ \beta_1</math> ist eine Bewegung. | ||
| − | === | + | ===Lösungidee, noch zu ergänzen!!=== |
| − | Voraussetzung:AB; <math>\beta_1 (AB) = A'B'</math>; <math>\beta_2 ( \beta_1 (AB)) = A''B''</math> | + | Voraussetzung:AB; <math>\beta_1 (AB) = A'B'</math>; <math>\beta_2 ( \beta_1 (AB)) = A''B''</math> <br /> |
| − | Behauptung: 1. A''B'' ist Abbild von AB | + | Behauptung: <br />1. <math>A''B''</math> ist Abbild von AB <br /> 2. Abstandsinvarianz<br /> |
| + | Teil 2: | ||
{| class="wikitable center" | {| class="wikitable center" | ||
| Zeile 17: | Zeile 18: | ||
|- | |- | ||
| (I) | | (I) | ||
| − | | <math>\ AB = A'B'</math> | + | | <math>\ |AB| = |A'B'|</math> |
| Voraussetzung + Def. Bewegung | | Voraussetzung + Def. Bewegung | ||
|- | |- | ||
| (II) | | (II) | ||
| − | | <math>\ A'B' = A''B''</math> | + | | <math>\ |A'B'| = |A''B''|</math> |
| Voraussetzung + Def. Bewegung | | Voraussetzung + Def. Bewegung | ||
|- | |- | ||
| (III) | | (III) | ||
| − | | <math>\ AB = A''B''</math> | + | | <math>\ |AB| = |A''B''|</math> |
| (1),(2), Transität der Streckenkongruenz | | (1),(2), Transität der Streckenkongruenz | ||
|- | |- | ||
| Zeile 33: | Zeile 34: | ||
|} | |} | ||
Der Beweis ist vermutlich unvollständig, da noch zu zeigen ist, dass es sich um eine Abbildung handelt. Gezeigt habe ich nur, dass die Abstandsinvarianz gegeben ist.--[[Benutzer:Tja???|Tja???]] 15:39, 21. Okt. 2010 (UTC) | Der Beweis ist vermutlich unvollständig, da noch zu zeigen ist, dass es sich um eine Abbildung handelt. Gezeigt habe ich nur, dass die Abstandsinvarianz gegeben ist.--[[Benutzer:Tja???|Tja???]] 15:39, 21. Okt. 2010 (UTC) | ||
| + | [[Category:Elementargeometrie]] | ||
Aktuelle Version vom 18. November 2010, 00:29 Uhr
Es seien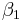 
und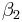 
zwei Bewegungen.
zu zeigen:
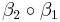ist eine Bewegung.
Lösungidee, noch zu ergänzen!!
Voraussetzung:AB;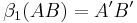 
; 
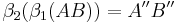
Behauptung:
1. 
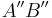ist Abbild von AB
2. Abstandsinvarianz
Teil 2:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |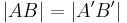 
|
Voraussetzung + Def. Bewegung |
| (II) |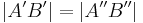 
|
Voraussetzung + Def. Bewegung |
| (III) |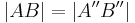 
|
(1),(2), Transität der Streckenkongruenz |
| (IV) |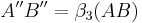 
|
(3)+ Def. Bewegung. |
Der Beweis ist vermutlich unvollständig, da noch zu zeigen ist, dass es sich um eine Abbildung handelt. Gezeigt habe ich nur, dass die Abstandsinvarianz gegeben ist.--Tja??? 15:39, 21. Okt. 2010 (UTC)
