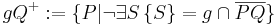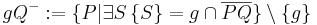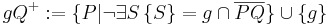Pasch: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Analogiebetrachtungen) |
*m.g.* (Diskussion | Beiträge) (→Definition IV.2: (Halbebene)) |
||
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 47: | Zeile 47: | ||
| colspan="2" | | | colspan="2" | | ||
<center>Klasse 1: </center> | <center>Klasse 1: </center> | ||
| − | <center> | + | <center> Menge aller Punkte von <math>\ G \setminus_{\{ T \}}</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ T </math> liegen </center> |
|- | |- | ||
| Zeile 56: | Zeile 56: | ||
| colspan="2" | | | colspan="2" | | ||
<center>Klasse 2:</center> | <center>Klasse 2:</center> | ||
| − | <center> | + | <center> Menge aller Punkte von <math>\ G \setminus_{\{ T \}}</math>, die bezüglich <math>\ Q</math> auf auf verschiedenen Seiten von <math>\ T</math> liegen </center> |
|- | |- | ||
| Zeile 99: | Zeile 99: | ||
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: <math>\ g Q^+</math>, (geschlossene) Halbebene: <math>\ g Q^+</math>. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass <math>\ g Q^+</math> bzw. <math>\ g Q^-</math> immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen. | Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene: <math>\ g Q^+</math>, (geschlossene) Halbebene: <math>\ g Q^+</math>. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass <math>\ g Q^+</math> bzw. <math>\ g Q^-</math> immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen. | ||
| − | |||
== Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | == Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen == | ||
| Zeile 107: | Zeile 106: | ||
===== Beweis des Satzes IV.1 ===== | ===== Beweis des Satzes IV.1 ===== | ||
| − | |||
'''Voraussetzung:''' <math>Q_2 \in {gQ_1}^{+} </math> | '''Voraussetzung:''' <math>Q_2 \in {gQ_1}^{+} </math> | ||
<br />'''Behauptung:''' <math>{gQ_1}^{+} \equiv {gQ_2}^{+}</math> und <math>{gQ_1}^{-} \equiv {gQ_2}^{-}</math> | <br />'''Behauptung:''' <math>{gQ_1}^{+} \equiv {gQ_2}^{+}</math> und <math>{gQ_1}^{-} \equiv {gQ_2}^{-}</math> | ||
| − | |||
| − | |||
| − | |||
| − | + | Üben Sie sich hier: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == | == Das Axiom von [http://de.wikipedia.org/wiki/Moritz_Pasch Pasch] == | ||
Aktuelle Version vom 28. November 2010, 18:51 Uhr
Inhaltsverzeichnis |
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |

|

|
 | |
| ? | ? |
 , das , das  in Klassen einteilt in Klassen einteilt | |
| ? | ? |
 | |
| ? | ? |
 teilt teilt 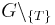 in genau zwei Klassen. Der Referenzpunkt in genau zwei Klassen. Der Referenzpunkt  hilft, diese Klassen anzugeben: hilft, diese Klassen anzugeben: | |
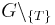 , die mit , die mit  auf derselben Seite von auf derselben Seite von  liegen liegen | |
| ? | ? |
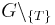 , die bezüglich , die bezüglich  auf auf verschiedenen Seiten von auf auf verschiedenen Seiten von  liegen liegen | |
| ? | ? |
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
Offene Halbebenen
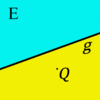
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt wird, heißen offene Halbebenen von
eingeteilt wird, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 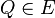 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit  auf derselben Seite liegen, wird mit
auf derselben Seite liegen, wird mit  bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und  mit
mit  .
.
Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich wirklicher mathematischer Exaktheit der Festlegung, was denn eine offene Halbene sein möge, bedarf es einer genauereren Erklärung, was denn darunter zu verstehen wäre, dass zwei Punkte  und
und  einer Ebene
einer Ebene  auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden
auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden  liegen.
liegen.
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
Halbebenen
Vereinigt man die Menge der Punkte einer offenen Halbeben mit der Menge der Punkte der Trägergerade so erhält man eine Halbebene.
Definition IV.2: (Halbebene)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene  .
.  und
und 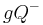 seien die beiden offenen Halbebenen von
seien die beiden offenen Halbebenen von  bezüglich
bezüglich  . Unter den (geschlossenen) Halbebenen von
. Unter den (geschlossenen) Halbebenen von  bezüglich
bezüglich  versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von
versteht die beiden Punktmengen, die durch die Vereinigung jeder dieser beiden offenen Halbebene von  bezüglich der Geraden
bezüglich der Geraden  mit jeweils dieser Geraden
mit jeweils dieser Geraden  entstehen.
entstehen.
- Es sei
Bemerkung: Für die formale Beschreibung von offenen und geschlossenen Halbebenen wird jeweils dieselbe Bezsichnung verwendet: offene Halbebene:  , (geschlossene) Halbebene:
, (geschlossene) Halbebene:  . Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass
. Derr weitere Gebrauch der Sprache kennzeichnet, ob es sich um eine offene oder um die geschlossene Halbene handeln soll. Aus Gründen der Vereinfachung sei vereinbart, dass  bzw.
bzw. 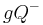 immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
immer die geschlossene Halbebene meint. Soll die offene Halbebene gemeint sein, so ist dieses durch den Zusatz "offen" zu kennzeichnen.
Die Repräsentantenunabhängigkeit des Referenzpunktes zweier Halbebenen
Repräsentantenunabhängigkeit?
Satz IV.1
- Wenn
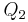 ein Punkt der Halbebene
ein Punkt der Halbebene 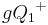 ist, dann gilt
ist, dann gilt 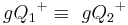 und
und  .
.
- Wenn
Beweis des Satzes IV.1
Voraussetzung: 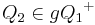
Behauptung: 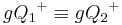 und
und 
Üben Sie sich hier:
Das Axiom von Pasch
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Hans Freudenthal, Mathematik als pädagogische Aufgabe, Stuttgart 1973, S. 14)
- Was Axiomatik ist und wie man Axiome zu formulieren hat, das ist erst gegen Ende des 19. Jh. von Pasch gezeigt worden; von ihm lernten es die italienischen Geometer und lernte es Hilbert.
Axiom III.2: Das Axiom von Pasch
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
- Gegeben sei ein Dreieck
Konvexe Punktmengen
Definition IV.3: (konvexe Punktmenge)
- Eine Menge
 von Punkten heißt konvex, wenn mit je zwei Punkten
von Punkten heißt konvex, wenn mit je zwei Punkten  und
und  dieser Menge die gesamte Strecke
dieser Menge die gesamte Strecke  zu
zu  gehört.
gehört.
- Eine Menge
Satz IV.2
- Halbebenen sind konvexe Punktmengen
Beweis von Satz IV.2
trivial (Der Leser überzeuge sich davon)
Satz IV.3
- Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Beweis von Satz IV.3
Es seien  und
und 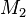 zwei konvexe Mengen.
zwei konvexe Mengen.
zu zeigen: Der Durchschnitt der beiden Mengen  und
und 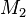 ist auch konvex.
ist auch konvex.
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 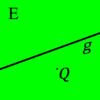
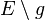 , die mit
, die mit