Übungsaufgaben 3 EG WS2010: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2) |
(→Aufgabe 2) |
||
| (20 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Alle Aufgaben beziehen sich auf die ebene Geometrie. | Alle Aufgaben beziehen sich auf die ebene Geometrie. | ||
==Aufgabe 1== | ==Aufgabe 1== | ||
| − | Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> den Punkt <math>\ Z</math> und nur den Punkt <math>\ Z</math> gemeinsam haben, dann gilt <math>S_h \circ S_g = D_{Z,\angle (g,h)}</math>. | + | Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> den Punkt <math>\ Z</math> und nur den Punkt <math>\ Z</math> gemeinsam haben, dann gilt <math>S_h \circ S_g = D_{Z,2|\angle (g,h)}|</math>.<br /><br /> |
| + | Gitl nicht: <math>S_h \circ S_g = D_{Z,\angle (g,h)*2}</math>?--[[Benutzer:Tja???|Tja???]] 10:00, 25. Nov. 2010 (UTC) | ||
| + | hab's gerade geändert--[[Benutzer:*m.g.*|*m.g.*]] 10:19, 25. Nov. 2010 (UTC) danke | ||
| + | |||
| + | ==Lösung von Aufgabe 1== | ||
| + | Wir zeigen zunächst, dass die Nacheinanderausführung <math>S_h \circ S_g</math> überhaupt eine Drehung ist. | ||
| + | |||
| + | Hierzu brauchen wir nur zu zeigen, dass <math>S_h \circ S_g</math> genau einen Fixpunkt hat, denn eine Bewegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt hat. Weil Z der einzige Punkt ist, der sowohl auf g als auch auf h liegt, ist er auch der einzige Fixpunkt von <math>S_h \circ S_g</math> (Der Leser überzeuge sich davon.) | ||
| + | |||
| + | Also ist <math>S_h \circ S_g</math> eine Drehung um den Fixpunkt Z. | ||
| + | |||
| + | Es bleibt zu zeigen, dass der Drehwinkel <math>\alpha</math> dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h (Reihenfolge beachten). | ||
| + | |||
| + | Hierzu reicht es zu zeigen, dass ein spezieller Punkt P mit P verschieden von Z derart durch <math>S_h \circ S_g</math> auf P' abgebildet wird, dass der Winkel <math>\angle P,Z,P'</math> doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h. | ||
| + | |||
| + | Begründung: | ||
| + | |||
==Aufgabe 2== | ==Aufgabe 2== | ||
| − | + | Es seien <math>\ g</math> und <math>\ h</math> zwei zueinander parallele Geraden. Ferner sei <math>\ a</math> eine Gerade, die senkrecht auf <math>\ g</math> und damit auch senkrecht auf <math>\ h</math> steht. Der Punkt <math>\ G</math> sei der Schnittpunkt von <math>\ a</math> mit <math>\ g</math> und der gemeinsame Schnittpunkt von <math>\ a</math> und <math>\ h</math> sei mit <math>\ H</math> bezeichnet. | |
| + | |||
| + | Man beweise: <math>S_h \circ S_g = V_{2 \overrightarrow{GH}}</math>.<br /> | ||
| + | <br /> | ||
| + | <br />==Beweis Aufgabe 2==<br /> | ||
| + | <ggb_applet width="882" height="498" version="3.2" ggbBase64="UEsDBBQACAAIACVcfT0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7ZnNcts2EMfPzVNweOjNNMAPgJxKziT2TOwZJ/bUaQ69QSRMoaZIlQRtyW/VJM+RZ+oCICVRkm3JclrXjS4UluAS+O1/FxDUez0ZZdY1LytR5H0bO8i2eB4XicjTvl3Ly73Qfn3wqpfyIuWDklmXRTlism97jmsrey0OXv3Uq4bFjcUy3eWT4Dd9+5JlFbetalxyllRDzmXHzuqJyAQrp2eDP3gsq/kN4+QkH9fwFlnWYItHyamo2ua+fuE4E/JIXIuEl1ZWxH2bBDB0+PaJl1LELOvbPjIWt2+7SzfB5Km7w6IUt0UuVfe580uwWFYlbjkQcZWtt68n2uN1nIlEsFxNRo8DOlnWjUjksG+HoQsuuUiHMFY/IsZbXBRlcjGtJB9Zk995WSinivPUNFyCVKuCYcH7At2YLra0F359waWEqFQWm/A5r7QUSadxUr0tsrlpXIhcHrKxrEsdUq8xXcipegG8q1TjfZOnGW9sMIl4yOOrQTG5MAw84/rjdKwf0QMapIdFVpRWqegG0KG5DsxV91EjnfVCug/SPRofyunsPo5c3UNfB+aqe2UiN0NrZo7bWWPUvkZUljIojKDE2eQzNuAQWduqcyFP2wYo4KqZKjYPfKhHA0iBRQ3MfOKn8tnbX1JP74qXOc+MRnKIbV3UlXWttGjepQeS8FiMoGluNEiYCtdvMABjTXha8nbgJoEMMH0XLepwydzbbwehxlDBWGMJlQDmI9VcVKJKSBL1LWFSWVQWZHzEIUWk1oOW04zLG3tWDwqd2svg5ojh/lpxaBmxbDxkYGn1n7EpZPrifLS/90XSnSXLgZaeAiTcWDlQ8RhzbkIpGwlbY3CoE2IBtSZUWRPIO8cjkIV9ew87BOrIwgec3JpCqZ8xyaSqgB6F10TaEHqA1duXwso1rAIn9LejExejEcsTK2cjeNUpJLpGIlT1txhScrIYVqQMhVq2N1LjqnGwAlrVjBnG1O6WETmEbM15VelaJxerWicYZvXZOBbo8ZGY0/QdHHU+Bi147MoQKYEC6j3XdQJKyXKpvGeO/M/c9KlMwRIjWExjIbeR7uGLkC7Gjj/jS55YuodGuumKdIdbSHf4kqXrUwe2TP4/LN2jFyFd2H+bqouB4S4LVFfHZyUs92mRs2yNoo/uUjTbQtHsP6To9dKdrpW6EnToINeni+anl3Y3Xie5hE0mAFoKVWpCxVZC9e7+UHVT5d1qqmwQBuLrOKjLwFx2j0QUONgnEcad2uK5TogwCoJOGDCFPRsO5lHwHpMJd5Ed3kX2eBuyx8+GrItgEXQpoi3awKDFDg3DkHiNNSQ7sb2PxfmjWDyzeuw6UWjWO9iPhbuU4PeiLItySXXnd5Xe85/ZuKh+2UZ77SP/KvU5OepQFxMS4CBAIY0oaTESF2whxQElLgWJPj3UBoRGO7wL7aMBPy/MOIDFKQwxDqMI+9SnM8yRTwMUhBHQJhEKdsF8wVNlXy/eFZ4d2oP7CVeN55bbYINtBH5wH7GQyt95I4Fxh7L52aHOAf1uTG7VyaRDfS+iNPI95HsU0022EXiDfYQGnqkqNlvdoO6tnjldcT5Wh31n+ceS5ZU68zV9Fs6yHrchGazE/RRvk1rQ+9ksnBTB7sPzI1gQiU9RcwiC1cqpahmCDsTzkDkSCZBDULSwcH6HPckauO5WcN1nAzegARQmqPsYij/CtGXrOwRHro8i+OGIIkKfjq0+Ab9vgQDpWcxtdtAdyt/+up+yPq2dQYTe6nkYU92MDDsB7L8i4rkEcj6MCNnl9w9Gq4ULbxgHvEmlafdNZTyHS1pjlhU3v/LLjE800E3Lxjr6GjhWwDX341Xun7fi/vlB7uEP7sjwxoq3xn7qrnL/shX3Lw9yxz+4IwMca+Aa/PkdG6VvX7ei//Uh+tT/H9DfX/x3S/+f2/yhffA3UEsHCB/7OjapBQAAAh8AAFBLAQIUABQACAAIACVcfT0f+zo2qQUAAAIfAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA4wUAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br /> | ||
| + | <br /> | ||
| + | Es sei <math>\ P</math> ein Punkt der Ebene mit <math>\ P \notin \ g, h</math> (Für <math>\ P \in \ g \ oder \ h</math> geht der Beweis analog) | ||
| + | <br /> | ||
| + | Wir haben zu zeigen: <br /> | ||
| + | 1. <math>\ PP'' \ || \ GH</math><br /> | ||
| + | 2. <math>\ 2| \overrightarrow{GH}| \ = \overline {|PP''|}</math><br /> | ||
| + | 3. Den Richtungssinn müssen wir, glaube ich, nicht zeigen, da klar ist, dass wir zuerst an g und danach an h spiegeln und somit klar ist, dass die "Richtung" von G nach H geht (stimmt das??)<br /> | ||
| + | <br /> | ||
| + | 1. Bei der Spiegelung von <math>\ P</math> an <math>\ g</math> erhalten wir den Lotfußpunkt <math>\ L1</math>. Bei der Spiegelung von <math>\ P'</math> an <math>\ h</math> erhalten wir den Lotfußpunkt <math>\ L2</math>.<br /> | ||
| + | Somit sind <math>\alpha ,\beta ,\gamma ,\delta</math> alle rechte Winkel und wir erhalten das Rechteck <math>\overline {GHL1L2}</math>.<br /> | ||
| + | <br /> | ||
| + | Daraus folgt, dass <math>\ L1L2 \ || \ GH</math>, woraus man folgern kann, dass <math>\ PP'' \ || \ GH</math> | ||
| + | <br /> | ||
| + | 2. <br /> | ||
| + | Beweis | ||
| + | {| class="wikitable " | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | | 1) <math>\overrightarrow{GH} \cong \overline {L1L2}</math> | ||
| + | | | ||
| + | |- | ||
| + | | 2) <math>|\overline {L1L2} | \ = \ | \overline {L1P'} | \ + \ | \overline {P'L2}| </math> | ||
| + | | Zwischenrelation (gilt nur für die Annahme, dass P in einer anderen Halbebene bezüglich g liegt wie h, für die anderen Fälle müsste der Beweis aber ähnlich ablaufen.) | ||
| + | |- | ||
| + | | 3) <math>\ 2| \overline {L1P'}| \ =\ | \overline {PP'}| </math> , <math>\ 2| \overline {P'L2}| \ =\ | \overline {P'P''}| </math> | ||
| + | | Definition Geradenspiegelung | ||
| + | |- | ||
| + | | 4) <math>\ | \overline {PP''}| \ =\ 2| \overline {L1L2}| \ =\ 2| \overline {GH}| </math> | ||
| + | | (1), (2), (3) | ||
| + | |||
| + | |- | ||
| + | |} - Steph85 | ||
| + | <br /><br /> | ||
| + | <br /> | ||
| + | |||
| + | ==Aufgabe 3== | ||
| + | Es seien <math>\ Z_1</math> und <math>\ Z_2</math> zwei nicht identische Punkte. Ferner seien die Winkel <math>\ \frac{\alpha}{2}</math> und <math>\ \frac{\beta}{2}</math> supplementär. | ||
| + | |||
| + | Man beweise: <math>D_{Z_2,\beta} \circ D_{Z_1, \alpha} = V_{2 \overrightarrow{Z_1Z_2}}</math>. | ||
| + | |||
| + | ===Beweis=== | ||
| + | Ist dieser Satz überhaupt korrekt?<br />--[[Benutzer:Tja???|Tja???]] 18:19, 28. Nov. 2010 (UTC) | ||
| + | Ich denke nicht. Zwar ist das Ergebnis zweier solcher Drehungen eine Verschiebung, die Richtung ist jedoch eine andere und die Länge ist auch eine andere(außer <math> \alpha = \beta = 180 </math>). | ||
| + | Hier ein Gegenbeispiel:<br /> | ||
| + | |||
| + | <ggb_applet width="699" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAO2UfD0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vldcts2EH5uToHhQ6Y/MQ2A/xMpGSV58YyTdGLX01HS6UAkLKGmSIUEbcmd3qnNEXqAnqkLgJJISVYk2+24qR5EcbEAFt9+u1hAnefTcYoueVGKPOtaxMYW4lmcJyIbdq1Knh+E1vNnjzpDng/5oGDoPC/GTHYtx6aWklfi2aOvOuUov0Is1Spngl91rXOWltxC5aTgLClHnMuWnFVTkQpWzN4OfuGxLJcNZpCjbFLBLLKoQBaPk2NRzl8P9YSTVMhX4lIkvEBpHnct3wPT4dcZL6SIWdq1XGwktGvRlUYQOap1lBfiOs+kUl8Ofg4ShEpxzQERqmSdQ73QDq/iVCSCZWox2g5QQuhKJHIEJkQRDMnFcAS2egSb0eI8L5KTWSn5GE37vMjBHOIpoGfmzTFvJdgFE3pYNzXf9DD88oRLCW4pEZvyJWDDQiStl6PyRZ4uRZNcZPIlm8iq0D51atGJnKkJYK5CGdzLhimvZRQgH/H4YpBPTwwIjhn6dDbRXbRBg+HLPM0LVCh4PVConwPz1DrK0oUW1jpYa9RjqEEX7SSiWkM/B+aptVKRGdPqlZP5qucQs6kokRIoGIGKi8WnbMDBtRaqMiGP5y9AgYt6qcR0eFONBxADTRIsxiT3NWbncIU+nQteZDw1JMnAt1VelehSkdHMpQ1JeCzG8GoaakiYctcPYICRJnxY8LnhJoIMYLq1RcQVcedwboSyoQRbYwmpANYj1VpUpEqIEvUrYVJJVBikfMwhRqTmg6bTApc+sRYZIdfBPQ/jWmEJMTRvJIemEUsnIwaSOf9TNoNQb65Hj/c6T9qrZBmgpZcAETdRAyh/TDhP6vQmaxKjCQypQ6IBtsaoRFPVz3MhDtUP30LXprPWMeGjAl/P69S+NZh8Dh36ZaDj2r5fo6Ng2geeOB+PWZagjI1hpmOIbQ2JUBkfMawZhBjRWBkgKjlvYmaweog1rFWiWCDJrHbukCMI0YyXpU5wspnKWu5oh/nn/YFv740m27AXtT6GfK4NG5CC94DaHnbd1YS4ZVH8Y2Z0SpOWxBj2zFjIfeja+zLYeoBttafMVK/gTnR9l0vIgiuE7Rm+EgoL/PbP3+GNahavsrf3mE3y8unPZDuLV1yw6HQbV/iu9oV6DMzjPrhKQxo4BDuRH3qBU1P1gNjUcZ0owGHkUY+G2Lt/pBdgaMSp20J8PV/U+ub7FqjXHR8K8p7tEBL5xKMupQH2Iw28Z1MSYur6vuNFJAzDu8Cu68DN/NZ5ma7QuAX3X39sx1hXLQvcQFv1B6uq2jZq4wgYBKUzdSKHRF6wIT/vnIAIXk/QZEfoyR6JlhVxA965ME3zq3f8POVTDalpbZSC++DfZj3wvOmHJbnbvvi0ly8+rfoCdp4wDCJMsRuEvhNh73/nixM+VPLN0bAd/cF28Mt65Dl0g1vWKi38G1vfP1qrHDg2UKKRcIJA5yEf8v9KdlKFC3Ft7DoQ1YFLfS/yneCeihgNeKq2/aNMwkmL65PL+gHqgvOJOrm+zU4LlpXqBmNXBrwSpWRZfENC3E4BNlB9k15L6zNbf1aNeSHiZQ27eYyVUA1s4vgh9jEOaUQ9HOxOArJWDU4nBXhC1Vy1Dad8KlcNQKDWtR5/rHL59EN+yQvlzF/NO/oOff0G0Hvf++mb5e9mfy03yr+hD09QV30tOt+wZnS4hpYEy6xtZt61eL1DuIjymJ3yH9tEA2skK+T3akc2EL4Wid6f3/eeoDZGtyLmtqOTgbVP+vRWHNQd1/cI2B6AewHGLgnJ/RNPz7oT2/qkQbc+3YljZvQdiLVY/H+ETX3yBAEG2zn0UhTxWq2hiwuy8fgSb+dNnGcN1sQP//S92wYkhjy7BNPyokRoiuuD5wybCdH1XDIl+pyp2kgtuiaNMhwOsoWYot5cvzfX6lFVwmMakeXh3wexU8/Qc2Fgc9/S8/Qcnrt5c4STcSzORbzd7YvNcsXzsXE8M8UlndvdIEDf2ecIBdoP5dwU2lCvND5OfXXltqSY3OXgdKY5clM+dtbArLZjaSi3wKq6jwLxX7rLCm04lzc+5uYFeEtI64arPqguZ9pldY1L7Jr1MeRAXgqWbc6J/bWdpu03XROm61cNzHiuWt9Id7lNaN9ENq4RHnRGfBD3kbu5p3eTe16INDmDBBePBB9U2XCflLXW96EksMB26HpIEdun+6Wsw+Z/PPpvzfp/3Wd/A1BLBwgVmNyGfwYAAAkeAABQSwECFAAUAAgACADtlHw9FZjchn8GAAAJHgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAALkGAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />A'' und das Bild der Verschiebung stimmen nicht über ein! | ||
Aktuelle Version vom 29. November 2010, 12:13 Uhr
Alle Aufgaben beziehen sich auf die ebene Geometrie.
Inhaltsverzeichnis |
Aufgabe 1
Beweisen Sie: Wenn die beiden Geraden  und
und  den Punkt
den Punkt  und nur den Punkt
und nur den Punkt  gemeinsam haben, dann gilt
gemeinsam haben, dann gilt 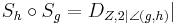 .
.
Gitl nicht: 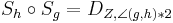 ?--Tja??? 10:00, 25. Nov. 2010 (UTC)
hab's gerade geändert--*m.g.* 10:19, 25. Nov. 2010 (UTC) danke
?--Tja??? 10:00, 25. Nov. 2010 (UTC)
hab's gerade geändert--*m.g.* 10:19, 25. Nov. 2010 (UTC) danke
Lösung von Aufgabe 1
Wir zeigen zunächst, dass die Nacheinanderausführung 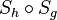 überhaupt eine Drehung ist.
überhaupt eine Drehung ist.
Hierzu brauchen wir nur zu zeigen, dass 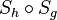 genau einen Fixpunkt hat, denn eine Bewegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt hat. Weil Z der einzige Punkt ist, der sowohl auf g als auch auf h liegt, ist er auch der einzige Fixpunkt von
genau einen Fixpunkt hat, denn eine Bewegung ist genau dann eine Drehung, wenn sie genau einen Fixpunkt hat. Weil Z der einzige Punkt ist, der sowohl auf g als auch auf h liegt, ist er auch der einzige Fixpunkt von 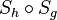 (Der Leser überzeuge sich davon.)
(Der Leser überzeuge sich davon.)
Also ist 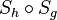 eine Drehung um den Fixpunkt Z.
eine Drehung um den Fixpunkt Z.
Es bleibt zu zeigen, dass der Drehwinkel  dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h (Reihenfolge beachten).
dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h (Reihenfolge beachten).
Hierzu reicht es zu zeigen, dass ein spezieller Punkt P mit P verschieden von Z derart durch 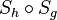 auf P' abgebildet wird, dass der Winkel
auf P' abgebildet wird, dass der Winkel 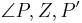 doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h.
doppelt so groß ist wie der Winkel zwischen den beiden Geraden g und h.
Begründung:
Aufgabe 2
Es seien  und
und  zwei zueinander parallele Geraden. Ferner sei
zwei zueinander parallele Geraden. Ferner sei  eine Gerade, die senkrecht auf
eine Gerade, die senkrecht auf  und damit auch senkrecht auf
und damit auch senkrecht auf  steht. Der Punkt
steht. Der Punkt  sei der Schnittpunkt von
sei der Schnittpunkt von  mit
mit  und der gemeinsame Schnittpunkt von
und der gemeinsame Schnittpunkt von  und
und  sei mit
sei mit 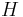 bezeichnet.
bezeichnet.
Man beweise: 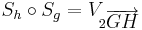 .
.
==Beweis Aufgabe 2==
Es sei  ein Punkt der Ebene mit
ein Punkt der Ebene mit 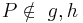 (Für
(Für 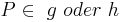 geht der Beweis analog)
geht der Beweis analog)
Wir haben zu zeigen:
1. 
2. 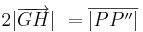
3. Den Richtungssinn müssen wir, glaube ich, nicht zeigen, da klar ist, dass wir zuerst an g und danach an h spiegeln und somit klar ist, dass die "Richtung" von G nach H geht (stimmt das??)
1. Bei der Spiegelung von  an
an  erhalten wir den Lotfußpunkt
erhalten wir den Lotfußpunkt 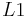 . Bei der Spiegelung von
. Bei der Spiegelung von  an
an  erhalten wir den Lotfußpunkt
erhalten wir den Lotfußpunkt 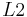 .
.
Somit sind 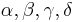 alle rechte Winkel und wir erhalten das Rechteck
alle rechte Winkel und wir erhalten das Rechteck 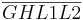 .
.
Daraus folgt, dass 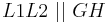 , woraus man folgern kann, dass
, woraus man folgern kann, dass 
2.
Beweis
| Beweisschritt | Begründung |
|---|---|
1) 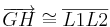
|
|
2) 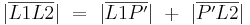
|
Zwischenrelation (gilt nur für die Annahme, dass P in einer anderen Halbebene bezüglich g liegt wie h, für die anderen Fälle müsste der Beweis aber ähnlich ablaufen.) |
3) 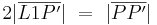 , , 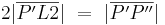
|
Definition Geradenspiegelung |
4) 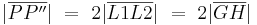
|
(1), (2), (3) |
Aufgabe 3
Es seien 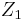 und
und 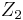 zwei nicht identische Punkte. Ferner seien die Winkel
zwei nicht identische Punkte. Ferner seien die Winkel 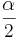 und
und 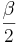 supplementär.
supplementär.
Man beweise: 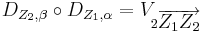 .
.
Beweis
Ist dieser Satz überhaupt korrekt?
--Tja??? 18:19, 28. Nov. 2010 (UTC)
Ich denke nicht. Zwar ist das Ergebnis zweier solcher Drehungen eine Verschiebung, die Richtung ist jedoch eine andere und die Länge ist auch eine andere(außer 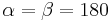 ).
Hier ein Gegenbeispiel:
).
Hier ein Gegenbeispiel:
A und das Bild der Verschiebung stimmen nicht über ein!

