Übungsaufgaben 4 EG WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 5) |
(→Aufgabe 4) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
Beweisen Sie mittels der Bewegung <math>S_b \circ S_a</math>, dass <math>\overline{ABC}</math> rechtwinklig ist. | Beweisen Sie mittels der Bewegung <math>S_b \circ S_a</math>, dass <math>\overline{ABC}</math> rechtwinklig ist. | ||
| − | [[Lösung]] | + | [[Lösung A4]] |
==Aufgabe 5== | ==Aufgabe 5== | ||
| Zeile 23: | Zeile 23: | ||
Jede Bewegung mit drei nichtkollineraren Fixpunkten ist gleichzeitig eine Verschiebung und eine Drehung. | Jede Bewegung mit drei nichtkollineraren Fixpunkten ist gleichzeitig eine Verschiebung und eine Drehung. | ||
| − | [[Lösung]] | + | [[Lösung A5]] |
Aktuelle Version vom 7. Dezember 2010, 15:02 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Interpretieren Sie das folgende Video:
Aufgabe 2
Es sei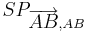 
eine Schubspiegelung.
Beweisen Sie: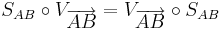 
Aufgabe 3
Es seien 
und 
zwei nichtidentische Geraden ein und derselben Ebene.
Beweisen Sie: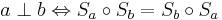 
.
Aufgabe 4
Es sei 
ein Dreieck und 
der Umkreis dieses Dreiecks.
Ferner seien 
ein Durchmesser von , die Mittelsenkrechte von 
und die Mittelsenkrechte von 
.
Beweisen Sie mittels der Bewegung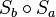 
, dass rechtwinklig ist.
Aufgabe 5
Beweisen Sie:
Jede Bewegung mit drei nichtkollineraren Fixpunkten ist gleichzeitig eine Verschiebung und eine Drehung.
