Lösung von Aufgabe 1.1 (SoSe 11): Unterschied zwischen den Versionen

Version vom 13. April 2011, 13:47 Uhr

In welchen Fällen handelt es sich um Definitionen? Begründen Sie!

1. Jedes n-Eck mit n=4 heißt Viereck.
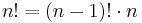2. , falls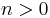
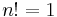   , falls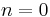
   
3. Stufenwinkel an geschnittenen Parallelen sind kongruent.
4. Jedes Dreieck mit einem Umkreis heißt Sehnendreieck.
5. Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
6. Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
7. Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
8. Jedes Viereck mit einem Umkreis heißt Sehnenviereck.
9. Es gibt Sehnenvierecke.
10. Punkt vor Strich.
11. Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
12. Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
13. Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
14. Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
15. Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
16. Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
17. Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
18. Ein Rechteck hat vier rechte Innenwinkel.
19. Ein Quadrat ist ein Rechteck.
20. Jedes Quadrat ist ein Rechteck.
21. Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.

1. ist eine Definition ( n-Eck ist der Oberbegriff-muss bekannt sein, Merkmal n= 4);
2. Definition ( Fakultät);
3. keine Definition, kann man beweisen;
4. Definition;
5. Definition ( gibt es Dreicksschneidende?) Anmerkung: Muss eine Definition immer sinnvoll sein, bzw. muss es etwas auch wirklich geben, wenn man es definiert? Was dies betrifft, sollte man sich auch 4. noch einmal genauer anschauen.--Andreas 13:44, 12. Apr. 2011 (CEST) ;
6. keine Definition - Aussage ?;
es ist ein Satz--Flo 21 00:31, 13. Apr. 2011 (CEST) 7. falsch - auch ein 5- Eck hat vier Ecken--Mathefix 11:59, 12. Apr. 2011 (CEST) es ist eine Def., aber eine unsinnige: Bei Def. gibt es kein richtig/falsch, sondern nur sinnvoll oder eben nicht sinnvoll --Flo 21 00:31, 13. Apr. 2011 (CEST) 8. Def.
9. Existenzaussage --> Satz
10. keine Def.
11. Satz des Thales
12. Def. aber man muss noch klären was kongruent und Nebenwinkel bedeuten
13. Def.
14. intuitive Def.
15. genetische Def. (Konstruktionsvorschrift)
16. Def. der Mittelsenkrechten
17. Def.
--Flo 21 00:31, 13. Apr. 2011 (CEST) 18. Aussage 19. Aussage 20. Aussage 21. Definition