Benutzer:Andreas: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Test) |
|||
| Zeile 73: | Zeile 73: | ||
==Test== | ==Test== | ||
| + | Satz: <math>a \| b \, \and\,b \| c \Rightarrow a\|c</math><br /> | ||
| + | Voraussetzung: a,b,c sind paarweise verschiedene Geraden; <math>a \| b \, \and\,b \| c</math><br /> | ||
| + | Annahme: <math> a\not\|c </math> | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | '''Beweisschritt''' || '''Begründung''' | ||
| + | |- | ||
| + | | 3 || 4 | ||
| + | |} | ||
Version vom 9. Mai 2011, 21:09 Uhr
Spiegelung_Test
Beweis Drehung
Inhaltsverzeichnis |
Satz: Jede Drehung 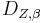 ist eine Bewegung.
ist eine Bewegung.
Beweis
Voraussetzung: Drehung D um Punkt Z mit dem Winkel 
Behauptung: |PQ|=|P'Q'|
| Beweisschritt | Begründung |
|---|---|
1) 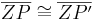
|
folgt unmittelbar aus der Definition: (Drehung) |
2) 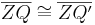
|
folgt unmittelbar aus der Definition: (Drehung) |
3) 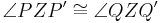
|
folgt unmittelbar aus der Definition: (Drehung) |
4) 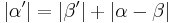
|
rechnen in den reellen Zahlen, folgt aus Schritt 3, da 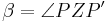 und und 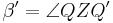
|
5) 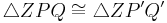
|
folgt aus den Schritten 1-4, sws |
6) 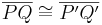
|
folgt aus Schritt 5 |
7) 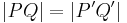
|
folgt aus Schritt 6, q.e.d |
--Andreas 14:22, 9. Nov. 2010 (UTC)
Satz: Wenn eine Bewegung  genau einen Fixpunkt Z hat, dann ist
genau einen Fixpunkt Z hat, dann ist  eine Drehung um den Fixpunkt Z.
eine Drehung um den Fixpunkt Z.
Beweis
Voraussetzung:  ist eine Bewegung,
ist eine Bewegung,  hat genau eine Fixpunkt Z
hat genau eine Fixpunkt Z
Behauptung: 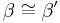
| Beweisschritt | Begründung |
|---|---|
1. 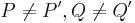
|
folgt unmittelbar aus der Voraussetzung (genau ein Fixpunkt Z) |
2. 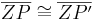
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
3. 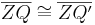
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
4. 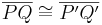
|
folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend) |
5. 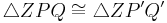
|
sss, folgt aus den Schritten 2-4 |
6. 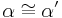 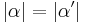
|
folgt aus Schritt 5 |
7.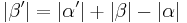  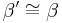
|
rechnen in den reellen Zahlen, Schritt 6 |
--Andreas 15:13, 11. Nov. 2010 (UTC)
Test
Satz: 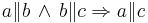
Voraussetzung: a,b,c sind paarweise verschiedene Geraden; 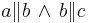
Annahme: 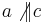
| Beweisschritt | Begründung |
| 3 | 4 |



