Lösung von Aufg. 8.1 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam. Category:Einführung_Geometrie“)
 
Zeile 1: Zeile 1:
 
Beweisen Sie: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
 
Beweisen Sie: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
  
 +
Voraussetzung: Ebene E und eine Gerade g, die nicht (vollständig) in E liegt <br />
 +
Behauptung: <math>\ E \cap g \ =  \ \lbrace \rbrace  \wedge  \lbrace S\rbrace</math>
 +
<br />
 +
Beweis in zwei Schritten:
  
 +
Fall 1: E und g haben keinen gemeinsamen Schnittpunkt: Dieser Fall ist trivial, genau dann wenn, g nicht mit E inzidiert und somit Parallel zur Ebenen e verläuft
 +
<br />
 +
Fall 2:  <math>\ E \cap g \ =  \ \lbrace S\rbrace</math>
 +
Beweis durch Widerspruch:
 +
Annahme: <math>\ E \cap g \ =  \ \lbrace S; P\rbrace</math>
 +
 +
 +
{| class="wikitable"
 +
|-
 +
| 1) S <math>\in</math> E|| Annahme
 +
|-
 +
| 2) P <math>\in</math> E || Annahme
 +
|-
 +
| 3) g liegt vollständig in E || Axiom I.5, (1), (2)
 +
|-
 +
| 4) Widerspruch zur Voraussetzung, Annahme ist zu verwerfen || (3), Voraussetzung
 +
|}
 +
--[[Benutzer:HecklF|Flo60]] 23:07, 31. Mai 2011 (CEST)
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 31. Mai 2011, 22:07 Uhr

Beweisen Sie: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.

Voraussetzung: Ebene E und eine Gerade g, die nicht (vollständig) in E liegt
Behauptung: 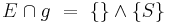\ E \cap g \ = \ \lbrace \rbrace \wedge \lbrace S\rbrace
Beweis in zwei Schritten:

Fall 1: E und g haben keinen gemeinsamen Schnittpunkt: Dieser Fall ist trivial, genau dann wenn, g nicht mit E inzidiert und somit Parallel zur Ebenen e verläuft
Fall 2: \ E \cap g \ = \ \lbrace S\rbrace Beweis durch Widerspruch: Annahme: \ E \cap g \ = \ \lbrace S; P\rbrace


1) S \in E Annahme
2) P \in E Annahme
3) g liegt vollständig in E Axiom I.5, (1), (2)
4) Widerspruch zur Voraussetzung, Annahme ist zu verwerfen (3), Voraussetzung

--Flo60 23:07, 31. Mai 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._8.1_(SoSe_11)&oldid=7534“