Lösung von Aufg. 9.5 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 30: Zeile 30:
  
  
 +
 +
9.6 Lösung:
 +
 +
Seien M1, M2 konvexe Mengen<br\>
 +
zz: <math>\ M1 \cap M2 =: M3 </math> ist konvex. <math>\Leftrightarrow</math> <math>\forall X,Q \in M3</math><math>\Rightarrow \overline{XQ}\subset M3</math><br\>
 +
Beweis:<br\>
 +
Seien <math>\operatorname X,Q \in M3 \Rightarrow  X,Q\in M1\ \wedge M2\Rightarrow \overline{XQ} \subset M1 \wedge M2</math>, da konvex.<math>\Rightarrow \overline{XQ} \subset M3 \Rightarrow</math> M3 ist konvex.--[[Benutzer:Peterpummel|Peterpummel]] 17:34, 19. Jun. 2011 (CEST)
  
 
[[Kategorie:Einführung_Geometrie]]
 
[[Kategorie:Einführung_Geometrie]]

Aktuelle Version vom 19. Juni 2011, 16:34 Uhr

Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
konvex bedeutet zunächst ja folgendes: 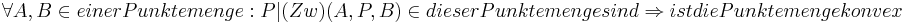\forall A, B \in einer Punktemenge: {P| \operatorname(Zw) (A, P, B)} \in dieser Punktemenge sind \Rightarrow ist die Punktemenge konvex

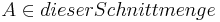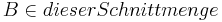
Voraussetzung: Zwei konvexe Punktmengen schneiden sich; A \in dieser Schnittmenge und B \in dieser Schnittmenge
Behauptung: 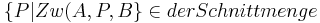\lbrace P| Zw(A, P, B\rbrace \in der Schnittmenge
Beweis durch Wiederspruch:
Annahme: 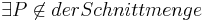\exists P \not\in der Schnittmenge

1 koll(A, B, P) Def. Strecke, Def. kollinear, Def. konvex
2 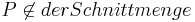P \not\in der Schnittmenge Annahme
3 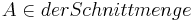A \in der Schnittmenge Voraussetzung
4 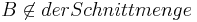B \not\in der Schnittmenge Def. konvex (P liegt zwischen A und B), Def. Strecke, Def. Zwischenrelation, (3), (2), (1)
5 Wiederspruch zur Voraussetzung, Annahme ist zu verwerfen (4)

--Flo60 15:43, 8. Jun. 2011 (CEST)
Der Beweis ist so nicht korrekt. Zunächst musst du deine Annahme genauer formulieren. Sonst kannst du Schritt 1 gar nicht machen.
Dann kannst du aus Schritt 2 und 3 nicht direkt auf Schritt 4 schließen, dieser Schluss muss in mehreren Schritten passieren. Diese Schritte sind dann auch wirklich ein Beweis.
Der Beweis kann auch direkt geführt werden.--Tutorin Anne 11:48, 11. Jun. 2011 (CEST)


9.6 Lösung:

Seien M1, M2 konvexe Mengen
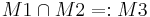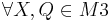
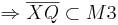
zz: \ M1 \cap M2 =: M3 ist konvex. \Leftrightarrow \forall X,Q \in M3\Rightarrow \overline{XQ}\subset M3
Beweis:
Seien 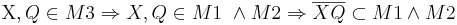\operatorname X,Q \in M3 \Rightarrow X,Q\in M1\ \wedge M2\Rightarrow \overline{XQ} \subset M1 \wedge M2, da konvex.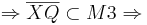\Rightarrow \overline{XQ} \subset M3 \Rightarrow M3 ist konvex.--Peterpummel 17:34, 19. Jun. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._9.5_(SoSe_11)&oldid=7714“