Die Umkehrung des Stufenwinkelsatzes (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes))
(→‎Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes))
Zeile 59: Zeile 59:
  
 
<br />stimmt das so? Ich finde, das ist sehr kurz, aber mir fällt weiter nichts dazu ein.  --[[Benutzer:Teufelchen|Teufelchen]] 21:01, 12. Jul. 2011 (CEST)<br /><br />
 
<br />stimmt das so? Ich finde, das ist sehr kurz, aber mir fällt weiter nichts dazu ein.  --[[Benutzer:Teufelchen|Teufelchen]] 21:01, 12. Jul. 2011 (CEST)<br /><br />
 +
<br />
 +
<br />
 +
und nun schon wieder ich :-) aus punkt eins und zwei folgt noch nicht, dass die die Winkel nicht kongruent sind. ich würde noch zwei schritte einbauen:
 +
 +
 +
Zusätzliche Voraussetzung: Seien die Schnittpunkte der Geraden A und B (weil die geschnittenen Geraden haben wir ja, sonst hätten wir keinen Stufenwinkel)
 +
 +
 +
Schritt 2.1 Es entsteht ein Dreieck /overline{ASB}. <math>\beta</math> ist Stufenwinkel von <math>\alpha</math> und ein Außenwinkel des Dreiecks overline{ASB}
 +
 +
 +
Begründung bei deinem Schritt 3: schwacher Außenwinkelsatz, Voraussetzung, Schritt 2.1
 +
 +
 +
Jetzt müsste es passen. --[[Benutzer:HecklF|Flo60]] 22:43, 12. Jul. 2011 (CEST)
 +
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 12. Juli 2011, 21:43 Uhr

Inhaltsverzeichnis

Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel

In welchen Fällen handelt es sich um....

Stufenwinkel
Wechselwinkel
entgegengesetzt liegende Winkel?

Definition X.1: (Stufenwinkel)

(ergänzen Sie)


Definition X.2: (Wechselwinkel)

(ergänzen Sie)


Definition X.3: (entgegengesetzt liegende Winkel)

(ergänzen Sie)
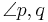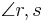Zwei Winkel \angle p,q und \angle r,s sind entgegengesetzt liegende Winkel, wenn der Stufenwinkel des Winkels 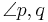\angle p,q und der Winkel Nebenwinkel sind. --Teufelchen 20:39, 12. Jul. 2011 (CEST)

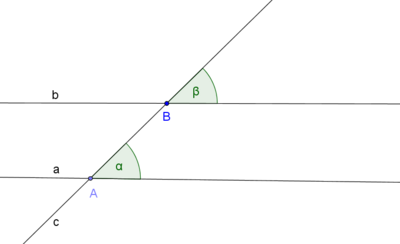
Die Umkehrung des Stufenwinkelsatzes

Satz X.1: (Umkehrung des Stufenwinkelsatzes)
Es seien \ a und \ b zwei nicht identische Geraden, die durch eine dritte Gerade \ c jeweils geschnitten werden. Es seien ferner \ \alpha und \ \beta zwei Stufenwinkel, die bei dem Schnitt von \ c mit \ a und \ b entstehen mögen.
Wenn die beiden Stufenwinkel \ \alpha und \ \beta kongruent zueinander sind, dann sind die Geraden \ a und \ b parallel zueinander.
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)

Es seien 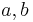\ a, b und \ c drei paarweise nicht identische Geraden. Die Gerade \ c möge \ a in dem Punkt \ A und die Gerade \ b in dem Punkt \ B schneiden. \ \alpha und \ \beta sei ein Paar von Stufenwinkeln, welches bei dem Schnitt von \ a und \ b mit \ c entstehen möge.

Voraussetzung:

(i) 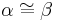\ \alpha \cong \beta

Umkehrung stufenwinkelsatz 01.png

Behauptung:

\ a \| b

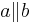
Annahme:

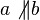
a\not\| b

Den Rest können Sie selbst!




Beweisschritt Begründung
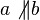1) a\not\| b Ann.
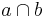2) \ a \cap b={S} 1), Satz Schnittpunkt von Geraden
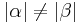3) |\alpha | \neq |\beta | (habe nicht kongruent nicht gefunden) 1,2
Widerspruch zur Vor., Ann. ist zu verwerfen, Beh. stimmt.


stimmt das so? Ich finde, das ist sehr kurz, aber mir fällt weiter nichts dazu ein. --Teufelchen 21:01, 12. Jul. 2011 (CEST)



und nun schon wieder ich :-) aus punkt eins und zwei folgt noch nicht, dass die die Winkel nicht kongruent sind. ich würde noch zwei schritte einbauen:


Zusätzliche Voraussetzung: Seien die Schnittpunkte der Geraden A und B (weil die geschnittenen Geraden haben wir ja, sonst hätten wir keinen Stufenwinkel)


Schritt 2.1 Es entsteht ein Dreieck /overline{ASB}. \beta ist Stufenwinkel von \alpha und ein Außenwinkel des Dreiecks overline{ASB}


Begründung bei deinem Schritt 3: schwacher Außenwinkelsatz, Voraussetzung, Schritt 2.1


Jetzt müsste es passen. --Flo60 22:43, 12. Jul. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Die_Umkehrung_des_Stufenwinkelsatzes_(SoSe_11)&oldid=8157“