Die Umkehrung des Stufenwinkelsatzes (SoSe 11)
Inhaltsverzeichnis |
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel
In welchen Fällen handelt es sich um....
- Stufenwinkel
- Wechselwinkel
- entgegengesetzt liegende Winkel?
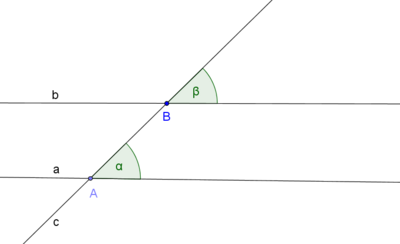
Definition X.1: (Stufenwinkel)
Zwei Winkel <(p,q) und <(r,s) heißen Stufenwinkel, falls ein Schenkel r des einen Winkels eine Teilmenge
eines Schenkels p des anderen Winkels ist und die anderen beiden Schenkel q und s in einer Halbebene
bezüglich der Geraden g liegen, die durch die beiden Schenkel p und r gegeben ist.--mm_l 11:56, 13. Jul. 2011 (CEST)
Die Definition ist noch nicht ganz korrekt. Weshalb? Ich denke, so sind auch manche Nebenwinkel des eigentlichen Stufenwinkels eingeschlossen.--Tutorin Anne 21:31, 14. Jul. 2011 (CEST)
Definition X.2: (Wechselwinkel)
Zwei Winkel <(p, q) und <(r, s) heißen Wechselwinkel, falls der Scheitelwinkel des Winkels <(p, q)
und der Winkel <(r, s) Stufenwinkel sind.--mm_l 11:58, 13. Jul. 2011 (CEST)
So geht's, oder?!
Wie könnte man Wechselwinkel ohne die Verwendung des Begriffes Stufenwinkel definieren?--Tutorin Anne 21:36, 14. Jul. 2011 (CEST)
Definition X.3: (entgegengesetzt liegende Winkel)
Zwei Winkel 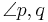 und
und 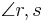 sind entgegengesetzt liegende Winkel, wenn der Stufenwinkel des Winkels
sind entgegengesetzt liegende Winkel, wenn der Stufenwinkel des Winkels 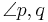 und der Winkel Nebenwinkel sind. --Teufelchen 20:39, 12. Jul. 2011 (CEST)
und der Winkel Nebenwinkel sind. --Teufelchen 20:39, 12. Jul. 2011 (CEST)
Der Nebenwinkel könnte doch auch ein Wechselwinkel sein... oder?
Also: Zwei Winkel <(p,q) und <(r,s) heißen entgegengesetzt liegende Winkel, falls der Nebenwinkel von <(r,s) Wechsel- oder Stufenwinkel von <(p,q) ist.--mm_l 12:10, 13. Jul. 2011 (CEST)
Gute Feststellung! Was meinen die Anderen?
Wie könnte man entgegengesetzt liegende Winkel ohne Verwendung von Stufen-/Wechselwinkel definieren?--Tutorin Anne 21:39, 14. Jul. 2011 (CEST)
Die Umkehrung des Stufenwinkelsatzes
Satz X.1: (Umkehrung des Stufenwinkelsatzes)
- Es seien
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von  mit
mit  und
und  entstehen mögen.
entstehen mögen.
- Wenn die beiden Stufenwinkel
 und
und  kongruent zueinander sind, dann sind die Geraden
kongruent zueinander sind, dann sind die Geraden  und
und  parallel zueinander.
parallel zueinander.
- Es seien
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)
Es seien 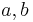 und
und  drei paarweise nicht identische Geraden. Die Gerade
drei paarweise nicht identische Geraden. Die Gerade  möge
möge  in dem Punkt
in dem Punkt und die Gerade
und die Gerade  in dem Punkt
in dem Punkt  schneiden.
schneiden.  und
und  sei ein Paar von Stufenwinkeln, welches bei dem Schnitt von
sei ein Paar von Stufenwinkeln, welches bei dem Schnitt von  und
und  mit
mit  entstehen möge.
entstehen möge.
Voraussetzung:
(i) 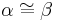
Behauptung:
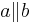
Annahme:
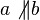
Den Rest können Sie selbst!
| Beweisschritt | Begründung |
1) 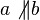 |
Ann. |
2) 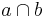 ={S} ={S} |
1), Satz Schnittpunkt von Geraden |
3) 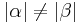 (habe nicht kongruent nicht gefunden) (habe nicht kongruent nicht gefunden) |
1,2 |
| Widerspruch zur Vor., Ann. ist zu verwerfen, Beh. stimmt. |
stimmt das so? Ich finde, das ist sehr kurz, aber mir fällt weiter nichts dazu ein. --Teufelchen 21:01, 12. Jul. 2011 (CEST)
und nun schon wieder ich :-) aus punkt eins und zwei folgt noch nicht, dass die die Winkel nicht kongruent sind. ich würde noch zwei schritte einbauen:
Zusätzliche Voraussetzung: Seien die Schnittpunkte der Geraden A und B (weil die geschnittenen Geraden haben wir ja, sonst hätten wir keinen Stufenwinkel)
Schritt 2.1 Es entsteht ein Dreieck 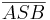 .
.  ist Stufenwinkel von
ist Stufenwinkel von  und ein Außenwinkel des Dreiecks
und ein Außenwinkel des Dreiecks 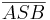
Begründung bei deinem Schritt 3: schwacher Außenwinkelsatz, Voraussetzung, Schritt 2.1
Jetzt müsste es passen. --Flo60 22:43, 12. Jul. 2011 (CEST)
Ja, genau das würde ich auch noch dazu sagen, dass ein Dreieck entsteht! --Herbst2010 11:23, 13. Jul. 2011 (CEST)
Ja, wir brauchen den schw. Außenwinkelsatz:
1) a geschnitten b => {C} nach Satz I.1
2)  ist Innenwinkel vom Dreick ABC nach Def. Innenwinkel
ist Innenwinkel vom Dreick ABC nach Def. Innenwinkel
3) ß ist Außenwinkel des Dreiecks ABC nach Def. Außenwinkel
4) ß >  nach dem schwachen Außenwinkelsatz was ein Widerspruch zur Voraussetzung ist.. somit gilt die Behauptung--mm_l 12:27, 13. Jul. 2011 (CEST)
nach dem schwachen Außenwinkelsatz was ein Widerspruch zur Voraussetzung ist.. somit gilt die Behauptung--mm_l 12:27, 13. Jul. 2011 (CEST)
Hallo, einmal eine wichtige Frage an euch: Wie seht ihr das? Wie kommt ihr auf die Idee über den schwachen Außenw.satz zu argumentieren? Wieso reichen meine Schritte nicht? Ich sehe das nicht. Ich habe zwar immer mal wieder das Gefühl, dass ein Beweis zu kurz ist, aber ich finde den Rest nicht. Soll ich mir immer Dreiecke basteln? Danke schon mal.
Du kannst es an der Stelle sehen, dass kein bisher bekannter Satz, keine Definition oder keiner der vorangegangenen Schritte deine letzte Aussage logisch begründet. An diesem Beispiel erklärt...
Du hast in dem Beweis geschrieben, dass a und b einen Schnittpunkt S haben. Daraus folgerst du, dass die Winkel nicht kongruent sind. Die Begründung für deine Folgerung sähe dann wie folgt aus...
Wenn zwei Geraden a und b nicht parallel sind bzw. sich in S schneiden, dann sind die Stufenwinkel nicht kongruent.
Das ist die Kontraposition vom zu beweisenden Satz, folglich ist es die gleiche Aussage wie der zu beweisende Satz und du beweist den Satz mit sich selbst. Was ich vorher an dieser Stelle geschrieben hatte, war nicht korrekt. Dies sollte dir helfen.--Tutor Andreas 22:07, 13. Jul. 2011 (CEST)
Satz: 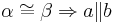
Kontraposition: 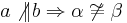
hmm, wenn ich das richtig verstehe, dann wäre mein Beweis richtig und vollständig, wenn wir den Stufenwinkelsatz bereits bewiesen hätten? Falls ja, wie kann das sein? Mit meinem Schnittpunkt, das verstehe ich z.T. ich hatte im Prinzip mein Dreieck konstruiert. Aber da ich aus der Parallelität rausgegangen bin und beide Geraden geschnitten habe, warum kann ich dann nicht folgern, dass die beiden eben nicht kongruent sind? Ich verstehe das nicht. Danke schon mal. --Teufelchen 20:56, 13. Jul. 2011 (CEST)
leider hilft mir das immer noch nicht, wie ich dann erkenne oder weiß, was ich noch machen muss, selbst wenn ich weiß, dass was fehlt. Mein Problem ist, dass mir die Idee fehlt oder vill das Wissen, keine Ahnung. Gibt das eine "Regel" nach der ich mir richten kann, wenn das, dann muss ich das machen, wenn aber jenes, dann eben jenes?? --Teufelchen 23:53, 13. Jul. 2011 (CEST)
Das ist nicht nur für dich ein Problem. Wie man einen Beweis führt, unterliegt keinem Algorithmus, wie z.B. das schriftliche Dividieren. Deshalb gibt es auch kein allgemeines Rezept und deshalb fällt es vielen so schwer... aber hier ein paar Tipps von mir, die ich für sinnvoll halte (zumindest in der Geometrie):
- Die Voraussetzung und die Behauptung aufschreiben und sich klar machen, was das bedeutet (wenn die Aussage z.B. komplett formal ist).
- Eine Skizze anfertigen und vllt. in einer Farbe markieren, was gegeben ist und in einer anderen Farbe die Behauptung kennzeichnen.
- Nun muss man noch eine Beweisidee finden... dies ist wohl der schwierigste Teil eines Beweises. Wenn man die Existenz von "Etwas" beweisen soll, dann kann man versuchen sich dieses "Etwas" mit Axiomen und Sätzen zu konstruieren. Bei der Eindeutigkeit liegt sehr oft ein indirekter Beweis sehr nahe. Bei einer "normalen" Implikation muss man sich oft "nur" klarmachen, was aus der Voraussetzung und bekannten Sätzen unmittelbar folgt. (garnicht so einfach das in Worte zu fassen...)
- Mein letzter Tipp klingt vllt. etwas altmodisch, aber ich kann nur sagen, dass es wirklich hilft... Übern, üben, üben und sich auch mal längere Zeit einem Beweis widmen und verschiedene Beweisideen ausprobieren, da man das Beweisen nicht durch nachvollziehen, sondern nur durch die eigene Auseinandersetzung mit der Materie lernen kann. Eben learning by doing :) --Tutor Andreas 12:01, 14. Jul. 2011 (CEST)
Sehr gute Tipps!
Ich denke, meist ist das aufschreiben des Beweis in Tabellen auch am sehr geeignet. Hier kann man am leichtesten sehen, wenn man keine Begründung hat.
Manchmal kann man den Beweis auch zusätzlich noch rückwärts anfangen (von unten), wenn man dafür schon Ideen hat.--Tutorin Anne 21:52, 14. Jul. 2011 (CEST)
@ Flo60: Musst du nicht erst deinen Punkt S konstruieren, indem du die Geraden a und b schneidest? Sonst hast du doch noch kein Dreieck, oder? Fragen über Fragen! --Teufelchen 16:18, 13. Jul. 2011 (CEST)
Um formal aufschreiben zu können, ist es besser, den Schnittpunkt von a und b mit S zu benennen. --Tutorin Anne 21:52, 14. Jul. 2011 (CEST)