Lösung von Aufg. 13.7 (SoSe 11): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Beweisen Sie:<br /> <u>Korollar 2 zum schwachen Außenwinkelsatz</u><br /> ::Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. …“) |
HecklF (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
::Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. | ::Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. | ||
| + | Ich finde, dass man diesen Beweis nicht führen kann! Mit dem schwachen Außenwinkelsatz ist dieser nicht möglich, da ich hierbei die Innenwinkelsumme haben MUSS. Das kann ich beweisen: | ||
| + | Wir gehen von folgendem "Beweis" aus. Dieser wird klassischerweise o.B.d.A. geführt (was schonmal den ersten Fehler in den Beweis bringt): | ||
| + | |||
| + | Voraussetzung: <math>\overline{ABC}</math> , <math>\alpha \beta \gamma</math> | ||
| + | Behauptung: Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. Mögen dies o. B. d. A. <math>\alpha und \beta</math> sein. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || Beta und Beta' sind Nebenwinkel, daraus folgt: <math>\beta + \beta ' = 180</math> || Außenwinkel Def., Nebenwinkel Def. supplementär, Suppl.Axiom | ||
| + | |- | ||
| + | | 2 || <math>\alpha < \beta '</math> || Schwacher Außenwinkelsatz, (1) | ||
| + | |- | ||
| + | | 3 || <math>\beta ' = 180 - \beta</math> || Rechnen in R, (1) | ||
| + | |- | ||
| + | | 4 || <math>180 - \beta > \alpha \Rightarrow \alpha +\beta < 180</math> || Rechnen in R, 2, 3 | ||
| + | |} | ||
| + | |||
| + | Und jetzt? q. e. d.? Von wegen. Dies muss ich noch für alle anderen machen, denn ansonsten ist sowas auch möglich: | ||
| + | |||
| + | [[Bild:dreieck2.JPG]] | ||
| + | |||
| + | |||
| + | Jetzt habe ich somit als Ergebnis: | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <math>\alpha + \beta < 180</math> | ||
| + | |- | ||
| + | | <math>\alpha + \gamma < 180</math> | ||
| + | |- | ||
| + | | <math>\beta + \gamma < 180</math> | ||
| + | |} | ||
| + | |||
| + | Insofern darf kein Dreieck die Innenwinkelsumme von 180 haben, was heißt, dass es kein Dreieck gibt - das kann die absolute Geometrie aber nicht wollen :-), das ist schlichtweg falsch. | ||
| + | |||
| + | Ergo: Einerseits zeigt der Beweis auf, dass entweder das vorkommen kann, was ich in der obigen Graphik eingeblendet habe, oder er zeigt an, dass die Innenwinkelsumme kleiner als 180 ist. Beides falsch - dass er Nebenbei auch noch aufzeigt, dass die Innenwinkelsumme von zwei Winkel jeweils kleiner ist als 180 ist schon klar, aber die "Kollateralschäden" die das Korrolar mit sich bringt sind doch aus meiner Sicht enorm. --[[Benutzer:HecklF|Flo60]] 19:09, 17. Jul. 2011 (CEST) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 17. Juli 2011, 18:09 Uhr
Beweisen Sie:
Korollar 2 zum schwachen Außenwinkelsatz
- Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Ich finde, dass man diesen Beweis nicht führen kann! Mit dem schwachen Außenwinkelsatz ist dieser nicht möglich, da ich hierbei die Innenwinkelsumme haben MUSS. Das kann ich beweisen:
Wir gehen von folgendem "Beweis" aus. Dieser wird klassischerweise o.B.d.A. geführt (was schonmal den ersten Fehler in den Beweis bringt):
Voraussetzung:  ,
, 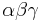 Behauptung: Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. Mögen dies o. B. d. A.
Behauptung: Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180. Mögen dies o. B. d. A. 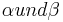 sein.
sein.
| 1 | Beta und Beta' sind Nebenwinkel, daraus folgt: 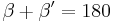 |
Außenwinkel Def., Nebenwinkel Def. supplementär, Suppl.Axiom |
| 2 | 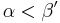 |
Schwacher Außenwinkelsatz, (1) |
| 3 | 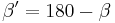 |
Rechnen in R, (1) |
| 4 | 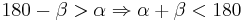 |
Rechnen in R, 2, 3 |
Und jetzt? q. e. d.? Von wegen. Dies muss ich noch für alle anderen machen, denn ansonsten ist sowas auch möglich:
Jetzt habe ich somit als Ergebnis:
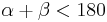
|
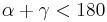
|
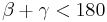
|
Insofern darf kein Dreieck die Innenwinkelsumme von 180 haben, was heißt, dass es kein Dreieck gibt - das kann die absolute Geometrie aber nicht wollen :-), das ist schlichtweg falsch.
Ergo: Einerseits zeigt der Beweis auf, dass entweder das vorkommen kann, was ich in der obigen Graphik eingeblendet habe, oder er zeigt an, dass die Innenwinkelsumme kleiner als 180 ist. Beides falsch - dass er Nebenbei auch noch aufzeigt, dass die Innenwinkelsumme von zwei Winkel jeweils kleiner ist als 180 ist schon klar, aber die "Kollateralschäden" die das Korrolar mit sich bringt sind doch aus meiner Sicht enorm. --Flo60 19:09, 17. Jul. 2011 (CEST)

