Lösung von Aufgabe 1.2 WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Tja??? (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
Den Rest können Sie alleine ... . | Den Rest können Sie alleine ... . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Kategorie:Elementargeometrie]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 18. Oktober 2011, 11:36 Uhr
Es seien  drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
(*) 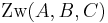 .
.
zu zeigen:
(**) 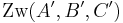
Wir übersetzen zunächst (*):
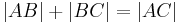
entsprechend (**) haben wir zu zeigen, dass 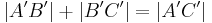 gilt.
gilt.
Den Rest können Sie alleine ... .

