Lösung von Aufgabe 3.5 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
Miriam (Diskussion | Beiträge) |
||
| Zeile 22: | Zeile 22: | ||
<math>\left| AC \right| = \left| BC \right| \wedge \left| CD \right| = \left| CD \right| \wedge \angle m, \overline{CA} = \angle m, \overline{CB}\Rightarrow \left| AD \right| = \left| BD \right|</math> SsW Die dreiecke sind konguent, somit muss auch der Abstand identisch sein. Somit liegt D auf m | <math>\left| AC \right| = \left| BC \right| \wedge \left| CD \right| = \left| CD \right| \wedge \angle m, \overline{CA} = \angle m, \overline{CB}\Rightarrow \left| AD \right| = \left| BD \right|</math> SsW Die dreiecke sind konguent, somit muss auch der Abstand identisch sein. Somit liegt D auf m | ||
| + | * So habe ich das auch gelöst, nur dass ich dabei mit SWS begründet habe. Außerdem könnte man das letzte "somit liegt D auf m" weglassen, da wir ja davon ausgegangen sind, dass D auf m liegt und nur beweisen müssen, dass jeder Punkt Element von m zu den Endpunkten der Strecke AB denselben Abstand hat. :)--[[Benutzer:Miriam|Miriam]] 17:00, 1. Nov. 2011 (CET) | ||
Annahme: | Annahme: | ||
Version vom 1. November 2011, 17:00 Uhr
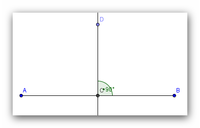
Der Begriff Mittelsenkrechte sei folgendermaßen definiert:
Die Mittelsenkrechte einer Strecke  ist die Gerade g, die durch den Mittelpunkt von
ist die Gerade g, die durch den Mittelpunkt von  verläuft und zu dieser Strecke
verläuft und zu dieser Strecke  senkrecht steht.
senkrecht steht.
Beweisen Sie folgenden Satz:
Die Mittelsenkrechte m einer beliebigen Strecke  ist die Menge aller Punkte P, die von A und B denselben Abstand haben:
ist die Menge aller Punkte P, die von A und B denselben Abstand haben:
(Beachten Sie, dass auch dieser Beweis wieder aus zwei Teilen besteht analog zur Aufgabe 3.4).
Voraussetzungen:
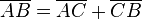 der Mittelpunkt der Strecke AB ist der Punkt C
der Mittelpunkt der Strecke AB ist der Punkt C
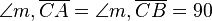 ° m ist die Mittelsenkrechte; D ein exemplarisch verwendeter Punkt auf m
° m ist die Mittelsenkrechte; D ein exemplarisch verwendeter Punkt auf m
Behauptung:
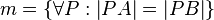 Alle Punke mit der Eigenschaft, dass der Abstand zu A und B gleich ist, bilden die Mittelsenkrechte
Alle Punke mit der Eigenschaft, dass der Abstand zu A und B gleich ist, bilden die Mittelsenkrechte
Beweis:
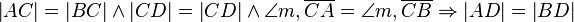 SsW Die dreiecke sind konguent, somit muss auch der Abstand identisch sein. Somit liegt D auf m
SsW Die dreiecke sind konguent, somit muss auch der Abstand identisch sein. Somit liegt D auf m
- So habe ich das auch gelöst, nur dass ich dabei mit SWS begründet habe. Außerdem könnte man das letzte "somit liegt D auf m" weglassen, da wir ja davon ausgegangen sind, dass D auf m liegt und nur beweisen müssen, dass jeder Punkt Element von m zu den Endpunkten der Strecke AB denselben Abstand hat. :)--Miriam 17:00, 1. Nov. 2011 (CET)
Annahme:
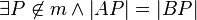
Beweis Teil 2:
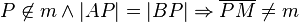 Es muss dan also eine Gerade geben welche die Punke P und M schneidet jedoch nicht die Mittelsenkrechte ist, sonst wäre ja P Element m
Es muss dan also eine Gerade geben welche die Punke P und M schneidet jedoch nicht die Mittelsenkrechte ist, sonst wäre ja P Element m
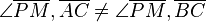 Da es dich nicht um die Mittelsenkrechte handelt, müssen die Winkel auch unterschiedlich sein.
Da es dich nicht um die Mittelsenkrechte handelt, müssen die Winkel auch unterschiedlich sein.
Fehler beim Parsen(Unbekannte Funktion „\lightning“): \overline{MP} =\overline{MP} \wedge \left| AP \right|= \left| PB \right| \wedge \overline{AC} = \overline{BC} \Rightarrow \angle \overline{PM},\overline{AC} = \angle \overline{PM},\overline{BC}\lightning
SSS - Wenn die drei Seiten des Dreiecks konguent sind müssen die Winkel es auch sein. Also muss P Element m sein. --RicRic