Fixpunkt, Fixpunktgerade, Fixgerade (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Definition) |
HecklF (Diskussion | Beiträge) (→Definition) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
=== Definition des Begriffs Fixpunkt einer Abbildung === | === Definition des Begriffs Fixpunkt einer Abbildung === | ||
===== Definition 3.1: (Fixpunkt einer Abbildung <math>\ \phi</math> )===== | ===== Definition 3.1: (Fixpunkt einer Abbildung <math>\ \phi</math> )===== | ||
| − | ::Ein Punkt <math>\ F</math> heißt Fixpunkt einer Abbildung <math>\ \phi</math>, wenn ... | + | ::Ein Punkt <math>\ F</math> heißt Fixpunkt einer Abbildung <math>\ \phi</math>, wenn <math>\phi (F)</math> auf F abgebildet wird. |
| + | <br />oder<br /> | ||
| + | ::Ein Punkt <math>\ F</math> heißt Fixpunkt einer Abbildung <math>\ \phi</math>, wenn <math>\phi (F) \equiv F</math><br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 22:06, 9. Nov. 2011 (CET) | ||
=== Richtig verstanden? === | === Richtig verstanden? === | ||
| Zeile 33: | Zeile 36: | ||
</quiz> | </quiz> | ||
| + | [[Diskussion zum Quiz]] | ||
== Fixgeraden == | == Fixgeraden == | ||
=== Beispiele/Gegenbeispiele === | === Beispiele/Gegenbeispiele === | ||
=== Definition === | === Definition === | ||
| − | + | <ggb_applet width="792" height="655" version="4.0" ggbBase64="UEsDBBQACAAIANtWaj8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANtWaj8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vhtb9s2EP7c/oqDPgwbFtui3ux0doumQLECaRvAXTHsGyUxMhtJ1ETKL0F//I6kZMtxmrcmRbGiCd+Od7yHd89Rmb5aFzksWS25KGcOGboOsDIRKS+zmdOo88HEefXy+TRjImNxTeFc1AVVMyfQkjydOWP3PInIcTCIAz8eBG4UDeKEskEahKkfuGEUBKkDsJb8RSk+0ILJiiZsnixYQU9FQpUxvFCqejEarVarYWdqKOpslGXxcC1RAR6zlDOn7bxAdXubVr4R91yXjP5+f2rVD3gpFS0T5oB2oeEvnz+brniZihWseKoWM2fiohsLxrMF+jSe+A6MtFCFgFQsUXzJJG7tDY3PqqgcI0ZLvf7M9iDfuuNAypc8ZfXMcYdkEnmhA6LmrFStAGkNjToV0yVnK6tL94yZwAElRB5TrQa+fgXP9Vw40g2xjYdNFNkl1865vm082wS2Ca1MYLcHVjSwMoGVCdD5JZc8ztnMOae5RNh4eV7jlW3HUm1yZs7TTuxcJkfok+SXKOxrUC3OOO+6R/onwp9AL4z2nSQ9q6pu7mm0Mzk+9u5u0vsuR/3OJgmOD2164TfcjG4wav2+i58k7EGLpsx/83Ng0b/JzasW7fj7DEbBD3FxOupSZdpmB8iFlm2jR7FC6nzxjyE81mFPIMTciMYY5SGQY2zGHmA2AAkhCHFIJhDpdgz+GBcC8GECWo74YJIjnOCvYGyURRCiMj07xpwEgoYCCH0gJqcCwEwCk5eYo56PEmEIIW7S5omnVfgRBBGO/AkEeEadkmOCgj5uxDGa98An4OvNZAxeBJHWRwKd6tFEHx1VehC5EBGtELMaM9pmM8pPwNfeRC1cvKwatQdRUqRdV4lqexcojXy0ozrLT3tM+Gya05jlWBzm+iYBljTXGWEMnYtSQXeJnp3LaloteCLnTCncJeELXdJTqtj6LUrLzraRTUQpz2qh3oi8KUoJkIjc3Z5Z5KTX97anxoHfWwj6C2FvIer1x9faFbgCjWRoX9SyE6dp+k5L7KgBkfxY5puTmtGLSvB9N6YjU2emrElynnJafsZg1VY0LtCVHUNXXdmJvHF3EFGn843ECIb1P6wWSFUkGB73/40d2Ngln4S6BsuE6nwLjvflJnj9m3YtdFHQWGDL7UXQNdv5lNU6gXuDd/JE5Lsp4+YbWqmmNg8D5MBaH/51meXMhIJhVay6yUUs1nMbA77V9WlT4ag9QZwZeAEpwAuxKmZtG9vWyOijbaVcI+MaCbcLKp5u14mGMmvb2LZGCqPUHq11lXRuErczw6UhLtdp06MjJR3juog3JVen3UDx5KJ1ldgNH5oiZttI2ddJHkvndHQllKYXrC5Z3kYuXmYjGmkTsRfUKUt4gUO70EJC9XX9hQewsynLatYdPDePLguYWXX7QXkwbVS9rUXxrlx+wli4coDpqDvlVCY1r3TMQYxsf8F2UZVySbFYpP19OtXQ9UQXBYRHaWgwCRu1ELV5VyF3YKszLGcFPqhAmfAyEbqF+bV5nmk8QcRfkL6u3sPuxnD92lgzUUnzakH1G671OqcbVu/hYPS9F+lVdBB84wImc2UegXi9FWM2MuyRsVOhQpNQe3SEgEtYW7OwadtL+zq3z1PtrE6yPf61s1duCsPH4nQLYm/+F4iFw/BREUtEUdAyhdK8YU6RUZxdSaWuDjSgRKNnkWlUt0CtqlbBAfianLbQ0kPs2/eYXe+5+i3s3YcjfxhvBsXLvqotlSos5hf4xSIN36uW2U3nT56mzDzkbKn5t7RbpOU3XlQ5T7i6OSjLpmA1T7au1wYaPG7THnrgD9tqeUOs3hMwckfAWjmZ6y87KDg6O0CkCqojD/XFEl8uCr9tkVXL3betvcu28uM3gkZ5rb+SOrhN55yve9SIbMcvkd3pXuY95B7ulFhuL7F6hWd3SeuqRmNaSwvxiQM4OXN+dY+g/s3Z55TRLWRz8jCy0R8YmW1i2zxezJu4enzKODN+73MGPSCL+c1ksQ/e/Ba2uB474tnHlml/DrL2hh6ZjJ+SsD/W+GzIREnza6h7bqn78Dbie1B3/JNQ9+Cg8iG6rq9v+8kZfB/zzwiCqK8vkycHWC9vxnpplXVoLm/jjR9dKbes8V2lsvfEbqFOaK2YxCd/W3EUjg2VWNJ9fTs/n7X8PIffYXlPej57EMM8BTv3KeKJGPo9r+uDeD37Fjec/UIrIf+4D193W35GTB8L0lH/s838EaT9I/7L/wBQSwcIDdVzfZUGAABhGAAAUEsBAhQAFAAIAAgA21ZqP9Y3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADbVmo/DdVzfZUGAABhGAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAACwHAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | |
| − | * Eine Gerade g, die bei der Abbildung <math>\phi</math> ... | + | * Eine Gerade g, die bei der Abbildung <math>\phi</math> auf sich selbst abgebildet wird, ist eine Fixgerade.<br /> |
| + | <br /> | ||
| + | <ggb_applet width="1366" height="607" version="4.0" ggbBase64="UEsDBBQACAAIAG2yaT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAG2yaT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vhtb9s2EP7c/oqDPte2KOrNhdOiDVCsQNYOSDcM+0ZLtMxGEjWR8kvRH78jKdmynXZJ2w3DjDgUdcd7eXjPkcni5a4qYcNbJWR95ZGp7wGvM5mLurjyOr2apN7LF08XBZcFX7YMVrKtmL7yQqMp8isv4pQSnpNJnLJkEqZ5PkkzQifzcJn6PPRXNMw8gJ0Sz2v5jlVcNSzjt9maV+xGZkxbx2utm+ez2Xa7nQ6uprItZkWxnO5U7gGGWasrr394juZOFm2pVQ98n8x+//nGmZ+IWmlWZ9wDk0InXjx9stiKOpdb2IpcrzFhmgYerLko1phUEoYezIxWg4g0PNNiwxWuHU1t0rpqPKvGaiN/4p6gPOTjQS42IuftledPaRQFaUDm84T4UWx8yFbwWve6pPc5G6wtNoJvnVnzZD3iIi1luWTGInz+DIEf+PDMDMQNAQ5x7ES+e+dTNwRuCN0QOZ3QLQ+dauh0QqcTUg82Qollya+8FSsVQijqVYvbd5grvS+5jad/ccyePMOclPiEytTHOnGY43vff2a+MX5DI5idJklGXnXbPdLp4JLQOH64z+C7MqWD03BOLn0G0RfyjL/i1CX+oESjEbboyv7Y74VH+rU0zz26+fc5jMN/JcXFbODKoqcHqLXR7ctH80oZwtA5RHNT9wQiJEecYJlHQOY4JAEgHYBEEEY4JSnEZkyAJigIgUIKRo9QsOyIUvwVJtZYDBEaM28TJCUQdBRCRIFYUoWAVAJLTCRpQFEjiiDCRcY9CYwJGkMY44ymEGKMhpMJQUWKC3GO7gOgBKhZTBIIYoiNPRIarsepCR1NBhD7EBNjEGmNlHZ0Rv0UqMkm7uESddPpE4iyKh8etWwOe4Ha2JCObc81qJOu+GRRsiUv8aS4NTsJsGGlYYR1tJK1hmETA/euaFmzFpm65VrjKgUf2YbdMM13b1BbDb6tbiZr9Usr9bUsu6pWAJks/UPMsiSj5+AQNU7oSBCOBdFIEI+ek3v9SpRApzj6l60a1FmevzUax9aASL6vy/3rlrO7RorTNBYze+gseJeVIhes/g2L1XgxuMDxDDL9ajiDomQ+RCLb/HavsIRh9wdvJfYqEk398Qfbz96J6LkITaqMGfZF/qkEybX/osi65pvDFrEdP2ZbtIbao8lb9VqWx1cWgGvW6K619wcMrzVZvaqLktsisf0WD+fsbil3t327drY+7Buc+S6CZWGBB2wOQRShQj8u3Wh1TGgHLd/q+FbDH8pN5Ac5mQdWw45LN1otrF8XWp8qGdIk/uBGKNvSfK8nztCuTPWbo76rhb4ZJlpkd32qxC1411VLfqihU5vkR9lczM6KbHHH25qXfU3jZnayU46io3LPeSYqnDpBDwkz2/UrBuDe5rxo+RB4ae9mDjAr9cfVevHamnrTyuptvfmAtXAWwGI2RLlQWSsaU3OwxHPgjh+rKheK4TGSj9cZEmLqmTkuEB5toEF6dnotW3v7wq6Co+FeySu8a4G25WUr9ADzK3uJM3iCXH7Exna+D8cdQ/m9tWarkpXNmpmbXp91yfa8PcHB2vtZ5ufoIPg2BWR5YwyY7W04d5XhQsaHBg1aQp00KgRcwQ5ZNg1SpLS5vQdY3J/cNd5dY026hmYnvdm9PdsrLCCH1N9g9vo/htm3IJZMIwtYME3iHwJYJquK1TnU9npzgy3FO562zDeVBowY8BwwnR4EzJnqDVxgb7rTAVl2CX1/VXso8v6DcX+/WimuDVipb7GaBPfuCj3HdkKmEZ2PP644QyzOs1MIgZ9gHPNkLEjD876s8c5wh38ZKXt46P6YsA8/iTzn9r7ozq0/a7dEuWYpqqYUmdB9jHgwmbqxcd82ghccu1nLMBX2GAZc/w8YEE3ncd8zovQfoMD7FjtxIWtW3kOGa0cGdkGG4hFkKL6JDBE5uUuY6aMJQR0hEvq1TRoR4p7K33+BJ7gPATanNAyP6hf3lBEf4m/nw3jvZuPj1F5b+//BvPgLUEsHCLYvJuTfBQAAIBIAAFBLAQIUABQACAAIAG2yaT/WN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAbbJpP7YvJuTfBQAAIBIAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAB2BgAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />--[[Benutzer:HecklF|Flo60]] 22:19, 9. Nov. 2011 (CET) | ||
| + | <ggb_applet width="1280" height="874" version="4.0" ggbBase64="UEsDBBQACAAIAEZ4aj8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAEZ4aj8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vltb9s2EP7c/QpCH/aptvkiUlLntMgLhhVI1wHZhmHfaIm22ciSJsqOPezH70hKthzHad0u7VA0aEyRPN3xnufueHHHr9aLHK1UbXRZnAVkiAOkirTMdDE7C5bNdBAHr15+N56pcqYmtUTTsl7I5iwIraTOzoJJOFUJ5elAxfARCp4NJOPJIM6mGU8STDijAUJro18U5c9yoUwlU3WTztVCXpepbJzhedNUL0aju7u7YWdqWNaz0Ww2Ga5NFiA4ZmHOgvbhBajbe+mOOXGKMRn98ebaqx/owjSySFWArAtL/fK7Z+M7XWTlHbrTWTMHh2kcB2iu9GwOThGM4awjK1YBJJVKG71SBl7uTZ3XzaIKnJgs7P4z/4TyrUMByvRKZ6o+C/CQRIwwIUKeCBoxmrAAlbVWRdMKk9boqFM3Xml15/XaJ2cyDFBTlvlEWpXon38QxRSj53YgfqAwCOG3sF/DzA/UD6EfuJcJ/euhFw29TOhlQjjjShs9ydVZMJW5ARB1Ma2BwO3cNJtcufO0Czv3yXPwyei/QZhhiBSPukP4uf0V8BvajdG+k6RntamXJxrtTBLM6YfbpJ9ik3U2KWWHJik/4qZ4BF1/hg/yk/egBVPun/s9sMjoCRb9/NMMivCzuDgedakybrMDmbmVbZls1MLYfGEJ4okNe4I45IaIIMo5IgkMEUWQDYhwFHKYkhgJO0aIRbARIoZiZOUIQy45eAwfYeSUCcRBmV2NICcRAUMh4gwRl1MhgkxCLi8hRykDCc4Rh5eseUKtCiZQKGDGYhTCGW1KRgQEGbwIczBPESOI2ZdJhKhAwuojoU11Edujg0qKBEaCWIWQ1ZDRPptBPkbMeiNauHRRLZs9iNJF1j02ZbXlAqShHu3Knq9Pe1Xx2TiXE5XDVXFjmURoJXObEc7QtCwa1JFI/dqsltVcp+ZGNQ28ZdA7uZLXslHrH0HadLadbFoW5pe6bC7LfLkoDEJpmePtmcuc9J7p9tQwYb2NsL/Bexui9xw9aLeEHbQ0CuyXtenEZZa9thK70gBIvi3yzUWt5G1V6n03xiN364zVMs11pmXxOwSrtWJxQdtLyJWr7hKKuehOUtbZzcZACKP1n6ouIQFEZO/djZ+FkRgmvZ/YFqNU2oTjeIj7Pwz437R7YbL3VhJ7c2q1pUWu1c7DWW3TuTd5bS7KfLfknL6UVbOsXdMAh6itJ+fFLFcuMFyJhRs5vZ2U6xsfEczr+nVTwQz7E0xmDmwEBYFyDgLtOPGjk7FH20phJ4OdBO5CTGfbfZJQJ+HGiR+dFMSsP1rrKuncJLgzo40rYzhok6UrUTbi7fW+LHRz3U0and62rhL/ws/LxURt42ZfJ/mvdI5H9wJrfKvqQuVtHAOZy3JpfFr2QjxTqV7A1G+0kEhL129wAL+aqVmtuoPnriHzgLld3I/Qg2Wn6se6XLwuVr9CLBwcALqyGuIDDmGrvd/e+dT5MDZprSsbkWgCN8Ot2sVcpo2EiyXrp5pNS1CSOpWNbixwkLDLZl7Wrh+DOgOjzcZcLaD5Qo0LPhe/WxLOXVtn0Ubl5B2Uuu1t6Pd3dML2g4HoQlbm1Vza1q+FJJcbVe+B5PS9KbP70HWgQNpXrncE7iulfNj4E8NDBQpdtu1VLmDDoLU3izbt+Ldv631Xa321GbhXqv3qPRohtjxMDtrFQhYZKtzlfQ3JE+zuEoktakhCQd6gMxS26CybbtN4da2SA/xtLm7hNZ8MP/5g8N9Op0Y1Fq/YwxU+xswhuqRFd7AztC0rDVxzt9DLG1f7mrbKuYefdJYp1+L4svtX4V8xPtf1osp1qpvHOXhbQ1jPykLmx9kwB0zIE5iQ72GiF3ifTsUjaA/IvWD+Amhf6jrNj6BMD1BOH0cZ6pROtzCmhzDv3wpPi/NHYahnqljBUaEvgj/scZsJG9xx1K2sSZscaEO6dCG9agSVrtZrdN7Jn3dS59DQDdw3DOesVXoedrrOeT/l7hNq21M91enHE8oOCM1OITT7RugRQpMvROjhjaROIVR9I/QIoUQ8IaO/uLZsn9D0gMmLx5nc7+0uPqq5INT/KeLG/7q/e093tztR70LEw5gTzmMeM8Lgb7uItu1IjBPBQ4LDhFH4fILW7yFSsgNSLk8h5fLrIIUMaRIREmFOQh4LyiNHCh3CCo55KIgIIxoy/plYUQesXJ3CytXXwoqIAf4kxoxRIbj92gFYYUNBo4gJDqtc8IQ8ASlvdF2X9T1WLo915pffy6o0P5yUOO0rX5yo92fB4LOkwYOIXxxD/OJ0xC/+h4gfuQwGn+M2eBDwq2OAX50O+NX/EPAjJWXwNDVl1P9Wy32f3P7v6Mt/AVBLBwj1HZ0q6AYAALodAABQSwECFAAUAAgACABGeGo/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAEZ4aj/1HZ0q6AYAALodAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAfwcAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />--[[Benutzer:HecklF|Flo60]] 15:03, 10. Nov. 2011 (CET) | ||
=== Richtig verstanden? === | === Richtig verstanden? === | ||
| Zeile 46: | Zeile 53: | ||
| − | * Eine Fixgerade f einer Abbildung <math>\phi</math> | + | * Eine Fixgerade f einer Abbildung <math>\phi</math> ist genau dann eine Fixpunktgerade bzgl. der Abbildung <math>\phi</math>, wenn gilt: <math>\forall P \in f: P = fix</math>--[[Benutzer:HecklF|Flo60]] 22:22, 9. Nov. 2011 (CET) |
| − | + | ||
=== Richtig verstanden? === | === Richtig verstanden? === | ||
| Zeile 62: | Zeile 68: | ||
</quiz> | </quiz> | ||
| − | + | [[und wieder Diskussion]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
[[Category:Elementargeometrie]] | [[Category:Elementargeometrie]] | ||
Aktuelle Version vom 10. November 2011, 15:03 Uhr
Inhaltsverzeichnis |
Fixpunkte
Beispiele/Gegenbeispiele
Definition des Begriffs Fixpunkt einer Abbildung
Definition 3.1: (Fixpunkt einer Abbildung  )
)
- Ein Punkt
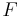 heißt Fixpunkt einer Abbildung
heißt Fixpunkt einer Abbildung  , wenn
, wenn 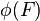 auf F abgebildet wird.
auf F abgebildet wird.
- Ein Punkt
oder
- Ein Punkt
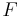 heißt Fixpunkt einer Abbildung
heißt Fixpunkt einer Abbildung  , wenn
, wenn 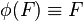
- Ein Punkt
--Flo60 22:06, 9. Nov. 2011 (CET)
Richtig verstanden?
Fixgeraden
Beispiele/Gegenbeispiele
Definition
- Eine Gerade g, die bei der Abbildung
 auf sich selbst abgebildet wird, ist eine Fixgerade.
auf sich selbst abgebildet wird, ist eine Fixgerade.
--Flo60 15:03, 10. Nov. 2011 (CET)
Richtig verstanden?
Fixpunktgeraden
Beispiele/Gegenbeispiele
Definition
- Eine Fixgerade f einer Abbildung
 ist genau dann eine Fixpunktgerade bzgl. der Abbildung
ist genau dann eine Fixpunktgerade bzgl. der Abbildung  , wenn gilt:
, wenn gilt: 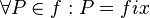 --Flo60 22:22, 9. Nov. 2011 (CET)
--Flo60 22:22, 9. Nov. 2011 (CET)

