Lösung von Aufg. 6.4 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
LGDo12 (Diskussion | Beiträge) |
|||
| Zeile 18: | Zeile 18: | ||
| Schritt || Begründung | | Schritt || Begründung | ||
|- | |- | ||
| − | | <math>\exists AB,BC,AC</math> || Vorraussetzung A,B,C koll Axiom I1 | + | | <math>\exists AB,BC,AC</math> || Vorraussetzung A,B,C koll Axiom I1 (Was ist mit A,B,C koll gemeint? Nach VSS gilt nkoll(A,B,C)).--[[Benutzer:Andreas|Tutor Andreas]] 15:04, 19. Nov. 2011 (CET) |
|- | |- | ||
| BC=AC || Annahme A=B | | BC=AC || Annahme A=B | ||
|- | |- | ||
| − | | AB=A=B || Annahme | + | | AB=A=B || Annahme (Diese Aussage finde ich etwas fragwürdig, denn nach Axiom I2 besteht jede Gerade aus mindestens 2 Punkten. Nach dieser Aussage würde aber eine Gerade existieren, die aus einem Punkt besteht, da A und B identisch sind bzw. wenn dies gelten würde, dann wäre doch streng genommen jeder Punkt eine Gerade... was sagen denn andere dazu?)--[[Benutzer:Andreas|Tutor Andreas]] 15:04, 19. Nov. 2011 (CET) |
|- | |- | ||
| koll(A,B,C) || Wiederspruch zur Voraussetzung, daraus folgt die Punke müssen paarweise verschieden sein. | | koll(A,B,C) || Wiederspruch zur Voraussetzung, daraus folgt die Punke müssen paarweise verschieden sein. | ||
| Zeile 37: | Zeile 37: | ||
| Schritt || Begründung | | Schritt || Begründung | ||
|- | |- | ||
| − | | <math>\exists AB,BC,AC</math> || Axiom I/1 | + | | <math>\exists AB,BC,AC</math> || Axiom I/1 (Das Axiom I1 liefert, um genau zu sein, keine 3 Geraden. Das heißt, die Begründung muss erweitert werden.)--[[Benutzer:Andreas|Tutor Andreas]] 15:04, 19. Nov. 2011 (CET) |
|- | |- | ||
| BC=AC || Voraussetzung A=B | | BC=AC || Voraussetzung A=B | ||
|- | |- | ||
| − | | AB=A=B || Voraussetzung | + | | AB=A=B || Voraussetzung (Diese Aussage finde ich etwas fragwürdig, denn nach Axiom I2 besteht jede Gerade aus mindestens 2 Punkten. Nach dieser Aussage würde aber eine Gerade existieren, die aus einem Punkt besteht, da A und B identisch sind bzw. wenn dies gelten würde, dann wäre doch streng genommen jeder Punkt eine Gerade... was sagen denn andere dazu?)--[[Benutzer:Andreas|Tutor Andreas]] 15:04, 19. Nov. 2011 (CET) |
|- | |- | ||
| − | | | + | | koll(A,B,C) || Axiom I/1 |
|} | |} | ||
<br /> | <br /> | ||
Version vom 19. November 2011, 16:04 Uhr
Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
- Wir formulieren Satz I neu und beginnen mit „Es seien
 ,
,  und
und  drei Punkte.“ Ergänzen Sie: „Wenn
drei Punkte.“ Ergänzen Sie: „Wenn  ,
, und
und  … , dann … .“
… , dann … .“
- Beweisen Sie Satz I indirekt.
- Bilden Sie die Kontraposition von Satz I.
- Beweisen Sie auch die Kontraposition von Satz I.
- Formulieren Sie die Umkehrung von Satz I.
- Gilt auch die Umkehrung von Satz I?
zu 1. Wenn A,B,C nicht kollinear sind, dann sind sie paarweise verschieden.
zu 2. Behauptung: A ungleich B ungleich C
Annahme: o.B.d.A. A = B
Beiweis:
| Schritt | Begründung |
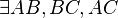 |
Vorraussetzung A,B,C koll Axiom I1 (Was ist mit A,B,C koll gemeint? Nach VSS gilt nkoll(A,B,C)).--Tutor Andreas 15:04, 19. Nov. 2011 (CET) |
| BC=AC | Annahme A=B |
| AB=A=B | Annahme (Diese Aussage finde ich etwas fragwürdig, denn nach Axiom I2 besteht jede Gerade aus mindestens 2 Punkten. Nach dieser Aussage würde aber eine Gerade existieren, die aus einem Punkt besteht, da A und B identisch sind bzw. wenn dies gelten würde, dann wäre doch streng genommen jeder Punkt eine Gerade... was sagen denn andere dazu?)--Tutor Andreas 15:04, 19. Nov. 2011 (CET) |
| koll(A,B,C) | Wiederspruch zur Voraussetzung, daraus folgt die Punke müssen paarweise verschieden sein. |
zu 3. Wenn A,B,C nicht paarweise verschieden, dann sind sie Kollinear.
zu 4. Voraussetzung Es seien drei Punkte A,B,C und o.B.d.A A=B
Behauptung: koll (A,B,C)
Beweis:
| Schritt | Begründung |
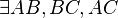 |
Axiom I/1 (Das Axiom I1 liefert, um genau zu sein, keine 3 Geraden. Das heißt, die Begründung muss erweitert werden.)--Tutor Andreas 15:04, 19. Nov. 2011 (CET) |
| BC=AC | Voraussetzung A=B |
| AB=A=B | Voraussetzung (Diese Aussage finde ich etwas fragwürdig, denn nach Axiom I2 besteht jede Gerade aus mindestens 2 Punkten. Nach dieser Aussage würde aber eine Gerade existieren, die aus einem Punkt besteht, da A und B identisch sind bzw. wenn dies gelten würde, dann wäre doch streng genommen jeder Punkt eine Gerade... was sagen denn andere dazu?)--Tutor Andreas 15:04, 19. Nov. 2011 (CET) |
| koll(A,B,C) | Axiom I/1 |
zu 5. Drei paarweise verschiedene Punkte sind nicht kollinar
zu 6. Nein, da auch Punkte existieren, welche koll sind und paarweise verschieden.--LGDo12 13:07, 17. Nov. 2011 (CET)

