Serie 05: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.1) |
||
| Zeile 3: | Zeile 3: | ||
<br /><br /> | <br /><br /> | ||
Es sei <math>\overline{A'B'C'_1</math> das Bild von <math>\overline{ABC}</math> bei einer Bewegung <math>\varphi</math>.<br /> | Es sei <math>\overline{A'B'C'_1</math> das Bild von <math>\overline{ABC}</math> bei einer Bewegung <math>\varphi</math>.<br /> | ||
| − | <math>\overline{A'_1B'_1C'_1</math> sei das Bild von <math>\overline{ABC}</math> bei der Spiegelung an der Mittelsenkrechten von <math>\overline{CC'_1}</math>. | + | <math>\overline{A'_1B'_1C'_1</math> sei das Bild von <math>\overline{ABC}</math> bei der Spiegelung an der Mittelsenkrechten von <math>\overline{CC'_1}</math>.<br /><br /> |
| + | Beweisen Sie: Die Mittelsenkrechte von <math>\overline{B'_1B'}</math> geht durch den Punkt <math>C'_1</math>. | ||
Version vom 22. November 2011, 13:28 Uhr
Aufgabe 5.1
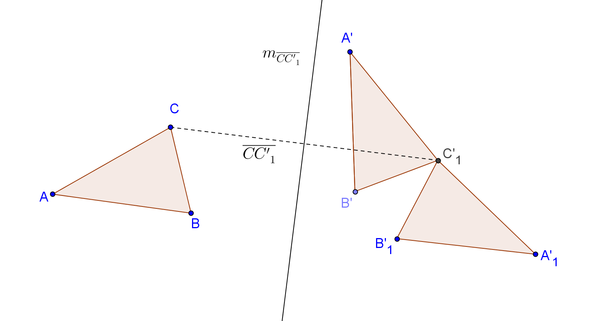
Es sei Fehler beim Parsen(Syntaxfehler): \overline{A'B'C'_1
das Bild vonbei einer Bewegung
.
Fehler beim Parsen(Syntaxfehler): \overline{A'_1B'_1C'_1
sei das Bild vonbei der Spiegelung an der Mittelsenkrechten von
.
Beweisen Sie: Die Mittelsenkrechte von 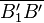 geht durch den Punkt
geht durch den Punkt 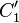 .
.

