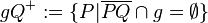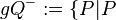Kleine Lücke: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „====Beispiel 1==== '''Definition IV.1: (offene Halbebene)''' :::Es sei <math>\ \varepsilon</math> eine Ebene in der die Gerade <math>\ g</math> liegen möge. Fern…“) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
:::Es sei <math>\ \varepsilon</math> eine Ebene in der die Gerade <math>\ g</math> liegen möge. Ferner sei <math>\ Q</math> ein Punkt der Ebene <math>\ \varepsilon</math>, der nicht zur Geraden <math>\ g</math> gehört.<br /> Unter den offenen Halbebenen <math>\ gQ^{+}</math> und <math>\ gQ^{-}</math> bezüglich der Trägergeraden <math>\ g</math> versteht man die folgenden Teilmengen der Ebene <math>\ \varepsilon</math> ohne die Gerade <math>\ g</math> : | :::Es sei <math>\ \varepsilon</math> eine Ebene in der die Gerade <math>\ g</math> liegen möge. Ferner sei <math>\ Q</math> ein Punkt der Ebene <math>\ \varepsilon</math>, der nicht zur Geraden <math>\ g</math> gehört.<br /> Unter den offenen Halbebenen <math>\ gQ^{+}</math> und <math>\ gQ^{-}</math> bezüglich der Trägergeraden <math>\ g</math> versteht man die folgenden Teilmengen der Ebene <math>\ \varepsilon</math> ohne die Gerade <math>\ g</math> : | ||
| − | ::::<math>\ gQ^{+}:= \{P|</math> ... | + | ::::<math>\ gQ^{+}:= \{P|</math> ''Ergänzen Sie selbst'' ... |
| + | ::::<math>\ gQ^{-}:= \{P|</math> ''Ergänzen Sie selbst'' ... | ||
| + | Nach Bearbeitung: | ||
| − | ::::<math>\ gQ^{-}:= \{P|</math> ... | + | ::::<math>\ gQ^{+}:= \{P| \overline{PQ} \cap g = \empty \}</math> |
| + | ::::<math>\ gQ^{-}:= \{P|P </math> | ||
| + | |||
| + | ====Beispiel 2==== | ||
| + | '''Definition V.2: (Inneres eines Winkels)''' | ||
| + | ::: Das Innere eines Winkels <math>\angle ASB</math> ist ... | ||
| + | |||
| + | Nach Bearbeitung durch eine/n Wikiuser/in:<br /> | ||
| + | '''Definition V.2: (Inneres eines Winkels)''' | ||
| + | ::: Das Innere eines Winkels <math>\angle ASB</math> die Vereinigungsmenge der beiden Halbebenen <math>ASB^+</math> und <math>BSA^+</math> | ||
Aktuelle Version vom 27. November 2011, 20:05 Uhr
Beispiel 1
Definition IV.1: (offene Halbebene)
- Es sei
 eine Ebene in der die Gerade
eine Ebene in der die Gerade  liegen möge. Ferner sei
liegen möge. Ferner sei  ein Punkt der Ebene
ein Punkt der Ebene  , der nicht zur Geraden
, der nicht zur Geraden  gehört.
gehört.
Unter den offenen Halbebenen und
und  bezüglich der Trägergeraden
bezüglich der Trägergeraden  versteht man die folgenden Teilmengen der Ebene
versteht man die folgenden Teilmengen der Ebene  ohne die Gerade
ohne die Gerade  :
:
- Es sei
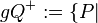 Ergänzen Sie selbst ...
Ergänzen Sie selbst ...
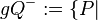 Ergänzen Sie selbst ...
Ergänzen Sie selbst ...
Nach Bearbeitung:
Beispiel 2
Definition V.2: (Inneres eines Winkels)
- Das Innere eines Winkels
 ist ...
ist ...
- Das Innere eines Winkels
Nach Bearbeitung durch eine/n Wikiuser/in:
Definition V.2: (Inneres eines Winkels)
- Das Innere eines Winkels
 die Vereinigungsmenge der beiden Halbebenen
die Vereinigungsmenge der beiden Halbebenen 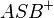 und
und 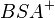
- Das Innere eines Winkels