Zentralprojektion, Parallelprojektion (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Satz II.03: Projektionssatz) |
*m.g.* (Diskussion | Beiträge) (→Beweisidee) |
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |
Aktuelle Version vom 16. Januar 2012, 11:33 Uhr
Zentralprojektionen
Wie kommt Lara Croft auf den Bildschirm?
Begriff der Zentralprojektion
Definition II.01: (Zentralprojektion des Raumes auf eine Ebene)
- Es sei
 eine Ebene des Raumes
eine Ebene des Raumes 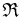 und
und  ein Punkt aus
ein Punkt aus 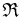 der nicht zu
der nicht zu  gehört.
gehört.
Die Zentralprojektion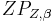 ist eine Abbildung von
ist eine Abbildung von 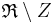 auf die Ebene
auf die Ebene  mit:
mit: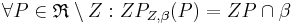
- Die Ebene
 heißt Bildebene bei der Zentralprojektion
heißt Bildebene bei der Zentralprojektion 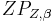 und der Punkt
und der Punkt  Zentralpunkt der
Zentralpunkt der 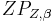 .
.
- Es sei
Definition II.02: (Zentralprojektion der Ebene auf eine Gerade)
- Versuchen Sie es selbst.
- Versuchen Sie es selbst.
Definition II.03: (Richtung)
- Eine Richtung ist eine Äquivalenzklasse nach der Relation "parallel" auf der Menge aller Geraden.
Definition II.04: (Parallelprojektion des Raumes auf eine Ebene)
- Es sei
 eine Ebene des Raumes
eine Ebene des Raumes 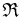 und
und 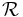 eine Richtung mit
eine Richtung mit 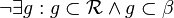 .
.
- Es sei
- Unter der Parallelprojektion des Raumes
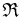 auf die Bildebene
auf die Bildebene  mit der Projektionsrichtung
mit der Projektionsrichtung 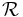 versteht man die Abbildung von
versteht man die Abbildung von 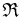 auf
auf  , die jedem Punkt
, die jedem Punkt 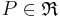 derart auf sein Bild
derart auf sein Bild  abbildet, dass gilt:
abbildet, dass gilt:
- Unter der Parallelprojektion des Raumes
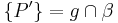 mit
mit 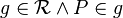
Definition II.05: (Parallelprojektion der Ebene auf eine Gerade)
- Es sei
 eine Gerade der Ebene
eine Gerade der Ebene 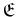 und
und 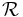 eine Richtung in
eine Richtung in 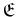 mit
mit 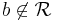 .
.
- Es sei
- Unter der Parallelprojektion der Ebene
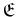 auf die Bildgerade
auf die Bildgerade  versteht man die Abbildung, die jeden Punkt
versteht man die Abbildung, die jeden Punkt 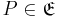 derart auf sein Bild
derart auf sein Bild  abbildet, dass gilt:
abbildet, dass gilt:
- Unter der Parallelprojektion der Ebene
 mit
mit 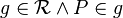 .
.
- In Zeichen:
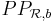
- In Zeichen:
Satz II.01: (Fixpunkte bei Parallelprojektionen)
- Es sei
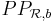 eine Parallelprojektion der Ebene auf die Gerade
eine Parallelprojektion der Ebene auf die Gerade  . Jeder Punkt der Bildgeraden
. Jeder Punkt der Bildgeraden  ist bezüglich
ist bezüglich 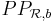 ein Fixpunkt.
ein Fixpunkt.
- Es sei
Satz II.02: Satz von der Mittelparallelen im Dreieck
- Es sei
 eine Dreieck mit den schulüblichen Bezeichnungen. Ferner seien
eine Dreieck mit den schulüblichen Bezeichnungen. Ferner seien 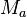 und
und 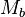 die Mittelpunkte der Seiten
die Mittelpunkte der Seiten  bzw.
bzw.  des Dreiecks
des Dreiecks  . Dann gilt:
. Dann gilt:
- (I)
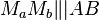
- (II)
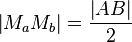
- Es sei
Satz II.03: Projektionssatz
- Es sei
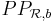 eine Parallelprojektion der Ebene auf die Gerade
eine Parallelprojektion der Ebene auf die Gerade  . Die Gerade
. Die Gerade möge
möge  in
in 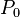 und nur in
und nur in 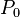 schneiden.
schneiden. 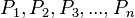 sei eine Folge von Punkten auf
sei eine Folge von Punkten auf  mit
mit 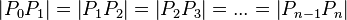 .
. 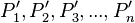 seiene die Bilder von
seiene die Bilder von 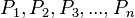 bei
bei 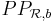 .
.
- Dann gilt:
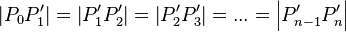 .
.
- Es sei
Beweisidee
Zeigen, dass die blauen Dreiecke zueinander kongruent sind.

