Lösung der Aufgaben zur Aussagenlogik (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Mahe84 (Diskussion | Beiträge) (→Aussagenlogik: table+) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 35: | Zeile 35: | ||
| <span style="color: red">f</span> | | <span style="color: red">f</span> | ||
| f | | f | ||
| − | | <span style="color: red"> | + | | <span style="color: red">f</span> |
|- | |- | ||
| w | | w | ||
| Zeile 42: | Zeile 42: | ||
| f | | f | ||
| <span style="color: red">w</span> | | <span style="color: red">w</span> | ||
| − | | | + | | |
|} | |} | ||
| − | <span style="color: red">Aussage | + | <span style="color: red">Aussage Äquivalent</span> |
| Zeile 95: | Zeile 95: | ||
<span style="color: red">Aussage Äquivalent</span> | <span style="color: red">Aussage Äquivalent</span> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
| + | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 19. April 2012, 11:00 Uhr
Aussagenlogik
Bitte rufen Sie sich die Aussagenlogik ins Gedächtnis. Eine gute Wiederholung (bzw. eine gute Einführung, falls Sie die mathematischen Grundlagen 1 noch nicht besucht haben) finden Sie bei youtube. Geben Sie dort "Spannagel Aussagenlogik" ein und sehen Sie sich Teil 1 bis 3 an.
Beweisen Sie mit einer Wahrheitstabelle:
- (A
 B)
B)  (
( 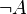
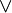 B)
B)
-
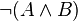
 (
(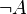
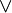
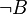 )
)
| A | B | (A  B) B)
|
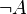
|
(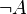 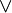 B) B)
| |
|---|---|---|---|---|---|
| f | f | w | w | w | |
| f | w | w | w | w | |
| w | f | f | f | f | |
| w | w | w | f | w |
Aussage Äquivalent
| A | B | 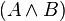
|
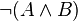
|
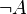
|
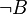
|
(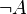 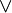 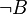 ) )
|
|---|---|---|---|---|---|---|
| f | f | f | w | w | w | w |
| f | w | f | w | w | f | w |
| w | f | f | w | f | w | w |
| w | w | w | f | f | f | f |
Aussage Äquivalent

