Lösung von Aufgabe 6.6: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(5 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Gegeben seien zwei nicht identische Punkte <math>\ A</math> und <math>\ B</math>. Unter <math>\ AB^-</math> wollen wir die Menge aller Punkte <math>\ P</math> verstehen, die man erhält, wenn man <math>\overline{A, B}</math> über <math>\ A</math> hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte <math>\ P</math> an.
+
Gegeben seien zwei nicht identische Punkte <math>\ A</math> und <math>\ B</math>. Unter <math>\ AB^-</math> wollen wir die Menge aller Punkte <math>\ P</math> verstehen, die man erhält, wenn man <math>\overline{A B}</math> über <math>\ A</math> hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte <math>\ P</math> an.
  
−
<math>AB^-:=\left \{ P| ...\right \}</math>}
+
Lösung: Ergänzen Sie einfach die folgende Mengenschreibweise:
 +
 
 +
<math>AB^-:=\left \{ P|Zw(P,A,B)\right \}\cup \left \{A \right \}</math>
 +
 
 +
diese Lösung ist richtig! --[[Benutzer:Schnirch|Schnirch]] 12:49, 16. Jun. 2010 (UTC)

Aktuelle Version vom 23. Juni 2010, 09:45 Uhr

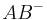Gegeben seien zwei nicht identische Punkte \ A und \ B. Unter \ AB^- wollen wir die Menge aller Punkte \ P verstehen, die man erhält, wenn man \overline{A B} über \ A hinaus verlängert. Geben Sie eine mathematisch korrekte Definition für die Menge dieser Punkte \ P an.

Lösung: Ergänzen Sie einfach die folgende Mengenschreibweise:

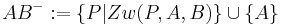
AB^-:=\left \{ P|Zw(P,A,B)\right \}\cup \left \{A \right \}

diese Lösung ist richtig! --Schnirch 12:49, 16. Jun. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_6.6&oldid=2211“