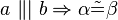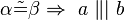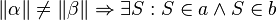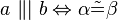Lösung von Aufgabe 2.2 S (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 2.2) |
(→Lösungsvorschlag 2) |
||
| (15 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | a) Stufenwinkelsatz: | + | ==== Lösungsvorschlag 1 ==== |
| + | a) Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.<br /> | ||
| + | b)<br /> | ||
| + | 1.) Wenn a parallel zu b, so sind Alpha und Beta kongruent.(entspricht Stufenwinkelsatz)<br /> | ||
| + | 2.) Wenn Alpha und Beta kongruent sind, so ist a zu b parallel .(entspricht '''nicht''' Stufenwinkelsatz)<br /> | ||
| + | 3.) Wenn Alpha und Beta nicht kongruent sind, so exsistiert ein Punkt S, der Element von a und b ist.(entspricht Sws.)<br /> | ||
| + | *Hier muss man aufpassen, da die Abkürzung Sws für einen anderen Satz benutzt wird. --[[Benutzer:Andreas|Tutor Andreas]] 15:09, 29. Apr. 2012 (CEST)<br /> | ||
| + | 4.) Genau dann wenn a parallel zu b, sind alpha und beta kongruent.(entspricht '''nicht''' Stufenwinkelsatz)[[Benutzer:Zigzag|Zigzag]]<br /> | ||
| + | *Bitte setzt eure Signatur hinter eure Beiträge. Dazu müsst ihr in der Werkzeugleiste den Button "Deine Signatur mit Zeitstempel" auswählen. --[[Benutzer:Andreas|Tutor Andreas]] 15:09, 29. Apr. 2012 (CEST) | ||
| − | b) 1.) Stufenwinkelsatz | + | ==== Lösungsvorschlag 2 ==== |
| − | + | a) Stufenwinkelsatz: Stufenwinkel an geschnitten Parallelen sind kongruent zueinander.<br /> | |
| − | + | b)<br /> | |
| − | + | 1.) Stufenwinkelsatz<br /> | |
| + | 2.) Umkehrung Stufenwinkelsatz<br /> | ||
| + | 3.) a und b schneiden sich in einem Punkt S<br /> | ||
| + | 4.) Stufenwinkelkriterium<br /> | ||
| − | Funkdocta | + | --[[Benutzer:Funkdocta|Funkdocta]] 15:09, 29. Apr. 2012 (CEST)<br /> |
| + | *Und welche Aussagen sind jetzt äquivalent zum Stufenwinkelsatz?--[[Benutzer:Andreas|Tutor Andreas]] 15:13, 29. Apr. 2012 (CEST) | ||
| + | <br /> | ||
| + | |||
| + | ''1) ist äquivalent, Stufenwinkelsatz<br /> | ||
| + | ''2) ist äquivalent, Umkehrung des Stufenwinkelsatz<br /> | ||
| + | ''3) nicht äquivalent<br /> | ||
| + | ''4) ist äquivalent, da Kriterium--[[Benutzer:Braindead|Braindead]] 15:56, 2. Mai 2012 (CEST)<br /> | ||
| + | *Was bedeutet denn '''äquivalent'''? Vielleicht kann das jemand an dieser Stelle mit einer Wahrheitstabelle verdeutlichen.--[[Benutzer:Andreas|Tutor Andreas]] 18:09, 2. Mai 2012 (CEST) | ||
| + | |||
| + | ==== Anmerkung zur Aufgabenstellung bei 3 ==== | ||
| + | |||
| + | Es hat in der heutigen Übung etwas irritiert, dass erst S definiert wird als Schnittpunkte der Geraden a und c, sowie b und c. Später wird S dann nochmal in einen anderen Kontext gebracht. Unklar ist, dass beide S anscheinend lediglich Schnittpunkte sind und keinen Zusammenhang besitzen. --[[Benutzer:Mathen00b|Mathen00b]] 12:44, 3. Mai 2012 (CEST) | ||
Aktuelle Version vom 3. Mai 2012, 14:07 Uhr
Inhaltsverzeichnis |
Aufgabe 2.2
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt S geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel 
und 
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
Lösungsvorschlag 1
a) Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.
b)
1.) Wenn a parallel zu b, so sind Alpha und Beta kongruent.(entspricht Stufenwinkelsatz)
2.) Wenn Alpha und Beta kongruent sind, so ist a zu b parallel .(entspricht nicht Stufenwinkelsatz)
3.) Wenn Alpha und Beta nicht kongruent sind, so exsistiert ein Punkt S, der Element von a und b ist.(entspricht Sws.)
- Hier muss man aufpassen, da die Abkürzung Sws für einen anderen Satz benutzt wird. --Tutor Andreas 15:09, 29. Apr. 2012 (CEST)
4.) Genau dann wenn a parallel zu b, sind alpha und beta kongruent.(entspricht nicht Stufenwinkelsatz)Zigzag
- Bitte setzt eure Signatur hinter eure Beiträge. Dazu müsst ihr in der Werkzeugleiste den Button "Deine Signatur mit Zeitstempel" auswählen. --Tutor Andreas 15:09, 29. Apr. 2012 (CEST)
Lösungsvorschlag 2
a) Stufenwinkelsatz: Stufenwinkel an geschnitten Parallelen sind kongruent zueinander.
b)
1.) Stufenwinkelsatz
2.) Umkehrung Stufenwinkelsatz
3.) a und b schneiden sich in einem Punkt S
4.) Stufenwinkelkriterium
--Funkdocta 15:09, 29. Apr. 2012 (CEST)
- Und welche Aussagen sind jetzt äquivalent zum Stufenwinkelsatz?--Tutor Andreas 15:13, 29. Apr. 2012 (CEST)
1) ist äquivalent, Stufenwinkelsatz
2) ist äquivalent, Umkehrung des Stufenwinkelsatz
3) nicht äquivalent
4) ist äquivalent, da Kriterium--Braindead 15:56, 2. Mai 2012 (CEST)
- Was bedeutet denn äquivalent? Vielleicht kann das jemand an dieser Stelle mit einer Wahrheitstabelle verdeutlichen.--Tutor Andreas 18:09, 2. Mai 2012 (CEST)
Anmerkung zur Aufgabenstellung bei 3
Es hat in der heutigen Übung etwas irritiert, dass erst S definiert wird als Schnittpunkte der Geraden a und c, sowie b und c. Später wird S dann nochmal in einen anderen Kontext gebracht. Unklar ist, dass beide S anscheinend lediglich Schnittpunkte sind und keinen Zusammenhang besitzen. --Mathen00b 12:44, 3. Mai 2012 (CEST)
