Lösung von Aufgabe 1.3 (SoSe 12): Unterschied zwischen den Versionen
(→5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.) |
(→Anmerkungen von Buchner zur Frage: Wie kann eine richtige Definition lauten?) |
||
| (16 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
Hier muss man unterscheiden, denn ein Radius und ein Abstand sind nicht das selbe. Vielleicht kann jemand dieses Unterschied an dieser Stelle erklären.--[[Benutzer:Andreas|Tutor Andreas]] 15:30, 26. Apr. 2012 (CEST) | Hier muss man unterscheiden, denn ein Radius und ein Abstand sind nicht das selbe. Vielleicht kann jemand dieses Unterschied an dieser Stelle erklären.--[[Benutzer:Andreas|Tutor Andreas]] 15:30, 26. Apr. 2012 (CEST) | ||
| + | Es gibt unendlich viele Punktmengen mit dem selben Abstand zu M. Nur die äußerste Menge wäre der Radius wenn man von einer Kugel ausging. ( so wie bei einer Zwiebel) --[[Benutzer:Wurzel|H2O]] 15:16, 30. Apr. 2012 (CEST) | ||
Zu 2.): | Zu 2.): | ||
| Zeile 65: | Zeile 66: | ||
====1.) Sei <math>M</math> ein Punkt und ''P'' eine Menge, deren Elemente Punkte sind. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist ''P'' ein Kreis mit Mittelpunkt ''M''. ==== | ====1.) Sei <math>M</math> ein Punkt und ''P'' eine Menge, deren Elemente Punkte sind. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist ''P'' ein Kreis mit Mittelpunkt ''M''. ==== | ||
| − | Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --[[Benutzer:Honeydukes|Honeydukes]] 13:20, 30. Apr. 2012 (CEST) | + | Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --[[Benutzer:Honeydukes|Honeydukes]] 13:20, 30. Apr. 2012 (CEST)so ist's.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:07, 8. Mai 2012 (CEST) |
====2.) Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis. ==== | ====2.) Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis. ==== | ||
| + | Die Ebene fehlt, könnte also auch eine Kugel werden. Und "für alle X gilt" fehlt auch und, dass es in P keine weiteren X gibt. Also, dass es nur die IXMI=r Punkte gibt und nicht noch andere, denn dann könnte es auch mehr als '''ein''' Kreis werden.<br /> (weiß jemand wie das umgedrehte, logische A geht?) --[[Benutzer:F4770n1|F4770n1]] 11:30, 6. Mai 2012 (CEST)<br /> | ||
| + | Gut! Das "für alle" geht so: Formelzeichen (n unter der Wurzel) und dann \forall : <br /><math> \forall</math> (drücke auf bearbeiten, um die Formel zu sehen.)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:10, 8. Mai 2012 (CEST) | ||
| + | |||
| + | Eine Frage: Für "alle X gilt" ist notwendig, weil es ansonsten mehr als ein Kreis geben könnte. Es fehlt doch dann aber immer noch die andere Richtung: für alle beliebigen Punkte, die die Bedingung erfüllen (den Abstand r) müssen auch in der Punktmenge sein. Ich bräuchte da nochmal Hilfe! (Anonymus) <br /> | ||
| + | * Bitte setzte als eine Unterschrift dahinter!! Was meinen die anderen?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 08:47, 12. Jun. 2012 (CEST) | ||
====3.) Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r <math>\epsilon </math> <math>\mathbb{R}^{+}</math> und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.==== | ====3.) Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r <math>\epsilon </math> <math>\mathbb{R}^{+}</math> und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.==== | ||
| + | Ich glaub auch nicht ganz, da nicht definiert ist, dass nur alle X = P sind. Also könnte auch wieder mehr als ein Kreis vorhanden sein, da P mehr ist als nur die X, die r ergeben. --[[Benutzer:F4770n1|F4770n1]] 11:30, 6. Mai 2012 (CEST)So ist's!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:11, 8. Mai 2012 (CEST) | ||
====4.) Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r<math>\epsilon </math><math>\mathbb{R}^{+}</math>, dann ist P ein Kreis.==== | ====4.) Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r<math>\epsilon </math><math>\mathbb{R}^{+}</math>, dann ist P ein Kreis.==== | ||
| Zeile 75: | Zeile 82: | ||
====5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.==== | ====5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.==== | ||
| − | Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? --[[Benutzer:Honeydukes|Honeydukes]] 13:20, 30. Apr. 2012 (CEST) | + | Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? --[[Benutzer:Honeydukes|Honeydukes]] 13:20, 30. Apr. 2012 (CEST) Ja!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:11, 8. Mai 2012 (CEST) |
| + | |||
| + | ====Wie kann eine richtige Definition lauten?==== | ||
| + | |||
| + | Ich hätte eine Frage bezüglich dieser Kreisaufgabe: | ||
| + | Die dritte Definition von Kreis ist ja nicht richtig, weil man nur eine Richtung beachtet hat. Wenn man aber "genau dann" (Äquivalenz" hinzufügen würde, wäre die Definition dann richtig? | ||
| + | Also: Sei M ein Punkt in der Ebene E und P eine Punktmenge. P ist genau dann ein Kreis mit Mittelpunkt M wenn für alle X Element P.... | ||
| + | Verstehe ich das so richtig? | ||
| + | |||
| + | ====Anmerkungen von Buchner zur Frage: Wie kann eine richtige Definition lauten?==== | ||
| + | Gut, dass Sie nochmal nachfragen. Zunächst nochmal zum Festhaten: Alle angegebenen Definitionen sind falsch. <br /><br /> | ||
| + | |||
| + | So wie Sie es vorschlagen klappt es nicht ganz, denn das würde bedeuten:<br /> | ||
| + | (1)Wenn für alle X Element von P gilt..., dann ist P ein Kreis.<br /> | ||
| + | (2) Wenn P ein Kreis ist, dann gilt für alle X Element von P...<br /><br /> | ||
| + | |||
| + | Den zweiten Teil wollen wir so nicht haben in einer Definition. [Zur Erinnerung: Eine Definition mit "wenn... dann" sieht so aus: "Wenn (Eigenschaften), dann (Begriff, der definiert werden soll)". Bei (2) wäre es grade umgekehrt, das wollen wir nicht in der Definition.<br /><br /> | ||
| + | Ihre Idee mit genau dann wenn ist aber gut, nur noch an der falschen Stelle.<br /> | ||
| + | Sie wollen ja aussagen: Alle X aus P haben denselben Abstand zu M. (das steht schon da) '''UND''' Es sind nur die X in P, die auch denselben Abstand zu M haben, und sonst keine. (das fehlt bei der dritten Definition, wie richtig festgestellt wurde).<br /><br /> | ||
| + | |||
| + | Sie haben jetzt mehrere Möglichkeiten für eine korrekte Definition:<br /> | ||
| + | (1) mit "genau dann wenn": Wenn ein Punkt X genau dann zu P gehört, wenn gilt ..., dann ist P ein Kreis.<br /> | ||
| + | (2) mit "alle und nur die": Wenn P alle und nur diejenigen Punkte X enthält, für die gilt..., dann ist P ein Kreis.<br /><br /> | ||
| + | |||
| + | --[[Benutzer:Buchner|Buchner]] 13:32, 11. Jun. 2012 (CEST) | ||
| + | |||
| + | Die (1) ist ja nur deshalb richtig, weil die Äquivalenz "genau dann wenn" drinsteckt, ansonsten wäre es ja wieder nur eine Richtung oder? Anonymous | ||
| + | <br /> | ||
| + | Ja. (1) und (2) sagen genau dasselbe aus.--[[Benutzer:Buchner|Buchner]] 17:45, 17. Jun. 2012 (CEST) | ||
Aktuelle Version vom 17. Juni 2012, 16:45 Uhr
Welche Definition für Kreis ist richtig? Warum (nicht)?
1.) Sei  ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:
ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist P ein Kreis mit Mittelpunkt M.
ist konstant, so ist P ein Kreis mit Mittelpunkt M.
2.) Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis.
3.) Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r 
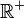 und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
4.) Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r
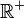 , dann ist P ein Kreis.
, dann ist P ein Kreis.
5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.
Zur 1.):
Ich hätte gesagt, dass die Definition falsch ist. Es ist die Rede von Mächtigkeit/ Betrag von MP, aber eigentlich müsste dastehen: Betrag der STRECKE von MP. (Ich wollte eine neue Formel einfügen, habe es aber nicht hinbekommen!) --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Meintest du sowas |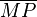 | ?--Tutor Andreas 18:40, 22. Apr. 2012 (CEST)
| ?--Tutor Andreas 18:40, 22. Apr. 2012 (CEST)
Ja, genau diese Formel meine ich. --Honeydukes 22:45, 22. Apr. 2012 (CEST)
Ich war gerade auf dem falschen Weg unterwegs.  geht ja überhaupt nicht! Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
geht ja überhaupt nicht! Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Ist hier mit dem Abstand nicht der Radius gemeint?--Braindead 10:29, 25. Apr. 2012 (CEST)
Hier muss man unterscheiden, denn ein Radius und ein Abstand sind nicht das selbe. Vielleicht kann jemand dieses Unterschied an dieser Stelle erklären.--Tutor Andreas 15:30, 26. Apr. 2012 (CEST)
Es gibt unendlich viele Punktmengen mit dem selben Abstand zu M. Nur die äußerste Menge wäre der Radius wenn man von einer Kugel ausging. ( so wie bei einer Zwiebel) --H2O 15:16, 30. Apr. 2012 (CEST)
Zu 2.):
Die Definition halte ich für fast richtig. Es fehlt meiner Meinung nach die Angabe "für alle X Element P". Ebenfalls weis man nicht, wo der Punkt x und die Punkte der Punktmenge liegen- Es fehlt der Hinweis auf die Ebene. --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Zu 3. und 4.):
Verstehe die Formeln nicht. Kann mir jemand sagen was R+ ist? Kann sie jemand formulieren, das würde mir weiterhelfen? --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Unterverstehen wir die Menge aller positiven reellen Zahlen.--Schnirch 13:42, 23. Apr. 2012 (CEST)
Hätte jetzt gesagt, dass die drei richtig ist! Für mich sind die beiden Definitionen bis auf X ∈ E in der 3.) gleich. Das fehlt in der 4.) --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Zu 5.):
Ich würde sagen, die Definition ist nicht korrekt. Ein Kreis ist eine geometrische Form in der Ebene (sonst könnte es eine Kugel sein). Bei einem Kreis befindet sich der Mittelpunkt auf gleicher Ebene wie die Punkte der Punktmenge (Jeder Kreis ist eine Menge von Punkten!). Alle diese Punkte der Punktmenge haben bei einem Kreis den gleichen Abstand zum Mittelpunkt (|MP| ist konstant). --Honeydukes 20:43, 21. Apr. 2012 (CEST)
Ja, ich habs gerade gemerkt. Hier ist das selbe Problem wir in 1.) zu sehen: Es gibt keinen Abstand zwischen einem Punkt und einer Menge (Punktmenge)! --Honeydukes 22:57, 24. Apr. 2012 (CEST)
Bei eiem Kreis wird doch nur eine Linie um einen Punkt beschrieben: "Die Menge an Punkten die von einem Punkt den selben Abstand haben". Bei einer Kugel sind es doch alle Punkte die zwischen Mittelpunkt und Außenlinie liegen und nicht nur die den selben Abstand haben. --Braindead 10:40, 25. Apr. 2012 (CEST)
Die Lösungen der Aufgabe stimmt so noch nicht alle - diskutiert und korrigiert euch selbst!--Tutorin Anne 11:57, 24. Apr. 2012 (CEST)(CEST)
Ich probier es auch mal.....
Ich hab mich auch mal mit dem ganzen hin und her, was ist hier richtig, was ist falsch rumgeschlagen....jetzt ist mir aber aufgefallen, dass
schon die Aufgabenstellung alles beantworten könnte. " Aufgabe 1.3....Welche Def. ist richtig?"
Eine Def. kann nur sinnvoll oder sinnlos sein...nicht richtig oder falsch. Also ist die Fragestellung falsch nicht die Def. Somit sind doch dann alle Def. hier sinnvoll oder sinnlos. Sollte ich richtig
liegen mit meiner Auslegung so könnten wir die Aufgabe umformulieren und diese so nennen. Welche der vier Aufgaben entspricht nicht einer formalen Def. und warum? --Kopernikus 22:02, 26. Apr. 2012 (CEST)
Eine Definition kann nur sinnvoll oder sinnlos sein - das stimmt. Bezogen auf unsere Vorstellung von Geometrie und die damit verbundene Vorstellung eines Kreises, dann man aber die Definitionen bewerten. Sie stimmen nicht, wenn sie math. nicht korrekt formuliert sind oder wenn die beschriebene Menge nicht unserer Vorstellung von Kreis entspricht.
Tip: Keine der Definitionen ist ganz korrekt. Fügt doch die Begründung jeweis direkt hinter die Definition--Tutorin Anne 10:53, 28. Apr. 2012 (CEST)
1.) Sei  ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:
ein Punkt und P eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist P ein Kreis mit Mittelpunkt M.
ist konstant, so ist P ein Kreis mit Mittelpunkt M.
Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? Ebenfalls fehlt, dass M und alle Elemente von P in der Ebene liegen. --Honeydukes 13:20, 30. Apr. 2012 (CEST)so ist's.--Tutorin Anne 10:07, 8. Mai 2012 (CEST)
2.) Sei M ein Punkt und P eine Punktmenge. Wenn gilt: X∈P∶ |XM|= r, dann ist P ein Kreis.
Die Ebene fehlt, könnte also auch eine Kugel werden. Und "für alle X gilt" fehlt auch und, dass es in P keine weiteren X gibt. Also, dass es nur die IXMI=r Punkte gibt und nicht noch andere, denn dann könnte es auch mehr als ein Kreis werden.
(weiß jemand wie das umgedrehte, logische A geht?) --F4770n1 11:30, 6. Mai 2012 (CEST)
Gut! Das "für alle" geht so: Formelzeichen (n unter der Wurzel) und dann \forall : 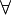 (drücke auf bearbeiten, um die Formel zu sehen.)--Tutorin Anne 10:10, 8. Mai 2012 (CEST)
(drücke auf bearbeiten, um die Formel zu sehen.)--Tutorin Anne 10:10, 8. Mai 2012 (CEST)
Eine Frage: Für "alle X gilt" ist notwendig, weil es ansonsten mehr als ein Kreis geben könnte. Es fehlt doch dann aber immer noch die andere Richtung: für alle beliebigen Punkte, die die Bedingung erfüllen (den Abstand r) müssen auch in der Punktmenge sein. Ich bräuchte da nochmal Hilfe! (Anonymus)
- Bitte setzte als eine Unterschrift dahinter!! Was meinen die anderen?--Tutorin Anne 08:47, 12. Jun. 2012 (CEST)
3.) Sei M ein Punkt in der Ebene E und P eine Punktmenge. Wenn für alle X∈P gilt∶ |XM|= r, r 
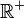 und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
und X ∈ E, dann ist P ein Kreis mit dem Mittelpunkt M.
Ich glaub auch nicht ganz, da nicht definiert ist, dass nur alle X = P sind. Also könnte auch wieder mehr als ein Kreis vorhanden sein, da P mehr ist als nur die X, die r ergeben. --F4770n1 11:30, 6. Mai 2012 (CEST)So ist's!--Tutorin Anne 10:11, 8. Mai 2012 (CEST)
4.) Sei M ein Punkt in der Ebene E und P eine Menge, deren Elemente Punkte sind. Wenn für alle X∈P gilt∶ |XM|= r, r
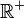 , dann ist P ein Kreis.
, dann ist P ein Kreis.
5.) Sei M ein Punkt und P eine Menge, deren Elemente Punkte sind. Alle Elemente von P liegen in ein und derselben Ebene wie M. Wenn gilt: |MP| ist konstant, so ist P ein Kreis mit Mittelpunkt M.
Es gibt keinen Abstand zwischen einem Punkt und einer Menge- nur zwischen zwei Punkten! Ist das korrekt? --Honeydukes 13:20, 30. Apr. 2012 (CEST) Ja!--Tutorin Anne 10:11, 8. Mai 2012 (CEST)
Wie kann eine richtige Definition lauten?
Ich hätte eine Frage bezüglich dieser Kreisaufgabe: Die dritte Definition von Kreis ist ja nicht richtig, weil man nur eine Richtung beachtet hat. Wenn man aber "genau dann" (Äquivalenz" hinzufügen würde, wäre die Definition dann richtig? Also: Sei M ein Punkt in der Ebene E und P eine Punktmenge. P ist genau dann ein Kreis mit Mittelpunkt M wenn für alle X Element P.... Verstehe ich das so richtig?
Anmerkungen von Buchner zur Frage: Wie kann eine richtige Definition lauten?
Gut, dass Sie nochmal nachfragen. Zunächst nochmal zum Festhaten: Alle angegebenen Definitionen sind falsch.
So wie Sie es vorschlagen klappt es nicht ganz, denn das würde bedeuten:
(1)Wenn für alle X Element von P gilt..., dann ist P ein Kreis.
(2) Wenn P ein Kreis ist, dann gilt für alle X Element von P...
Den zweiten Teil wollen wir so nicht haben in einer Definition. [Zur Erinnerung: Eine Definition mit "wenn... dann" sieht so aus: "Wenn (Eigenschaften), dann (Begriff, der definiert werden soll)". Bei (2) wäre es grade umgekehrt, das wollen wir nicht in der Definition.
Ihre Idee mit genau dann wenn ist aber gut, nur noch an der falschen Stelle.
Sie wollen ja aussagen: Alle X aus P haben denselben Abstand zu M. (das steht schon da) UND Es sind nur die X in P, die auch denselben Abstand zu M haben, und sonst keine. (das fehlt bei der dritten Definition, wie richtig festgestellt wurde).
Sie haben jetzt mehrere Möglichkeiten für eine korrekte Definition:
(1) mit "genau dann wenn": Wenn ein Punkt X genau dann zu P gehört, wenn gilt ..., dann ist P ein Kreis.
(2) mit "alle und nur die": Wenn P alle und nur diejenigen Punkte X enthält, für die gilt..., dann ist P ein Kreis.
--Buchner 13:32, 11. Jun. 2012 (CEST)
Die (1) ist ja nur deshalb richtig, weil die Äquivalenz "genau dann wenn" drinsteckt, ansonsten wäre es ja wieder nur eine Richtung oder? Anonymous
Ja. (1) und (2) sagen genau dasselbe aus.--Buchner 17:45, 17. Jun. 2012 (CEST)

