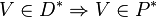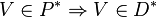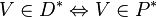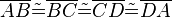Lösung von Aufgabe 2.3 S (SoSe 12): Unterschied zwischen den Versionen
Wurzel (Diskussion | Beiträge) (→Aufgabe 2.3) |
*m.g.* (Diskussion | Beiträge) (→Der eigentliche Beweis) |
||
| (47 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Aufgabe 2.3== | ==Aufgabe 2.3== | ||
Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?<br /> | Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?<br /> | ||
| + | ==Lösungsvorschläge== | ||
| + | ===ZigZag=== | ||
*Dass die Schnittmenge C der Mengen A und B alle Elemente der Mengen A und B beinhaltet.[[Benutzer:Zigzag]]<br /> | *Dass die Schnittmenge C der Mengen A und B alle Elemente der Mengen A und B beinhaltet.[[Benutzer:Zigzag]]<br /> | ||
| − | + | ===Wurzel alias H<sub>2</sub>O=== | |
| − | + | *A ist Teilmenge von B und B ist Teilmenge von A Dan ist A gleich B KeinKurpfälzer und --[[Benutzer:Wurzel|H2O]] 16:14, 30. Apr. 2012 (CEST) | |
| − | + | ===TiCron=== | |
| − | + | *Zwei Mengen sind identisch, wenn sie die selben Elemente enthalten. Kein Widerspruch zu H20 und KeinKurpfälzer. | |
| − | * | + | ==Bemerkungen M.G.== |
| + | ===Kommentar=== | ||
| + | Das ist soweit alles richtig, aber vielleicht noch nicht so wirklich hilfreich bezüglich des Führens von Beweisen.<br /> | ||
| + | Zunächst die Definition aus dem Skript:<br /> | ||
| + | [[Datei: Mengenlehre.pdf]] | ||
| + | {{Definition|Mengengleichheit<br />Zwei Mengen sind genau dann gleich, wenn sie aus denselben Elementen bestehen.}} | ||
| + | |||
| + | Diese Definition entspricht dem Beitrag von TiCron. | ||
| + | |||
| + | Auch in der Kurpfalz gilt jetzt das, was Team <math>\left{ \operatorname{Wasser, nicht aus der Kurpfalz}\right}</math> formuliert:<br /><br /> | ||
| + | '''Satz:'''<br /> | ||
| + | ::Es seien <math>A</math> und <math>B</math> zwei Mengen. Wenn <math>A \subset B \wedge B \subset A</math>, dann <math>A=B</math>.<br /> | ||
| + | ZigZag drückt das so aus:<br /><br /> | ||
| + | '''Satz:'''<br /> | ||
| + | ::<math>A \cap B = A \wedge A \cap B = B \Rightarrow A=B</math>. | ||
| + | |||
| + | Beide Sätze könnten auch als Kriterium formuliert (gdw.) und somit als Definition verwendet werden. | ||
| + | |||
| + | Was muss ich aber konkret machen, wenn ich zeigen will, dass zwei Mengen <math>A</math> und <math>B</math> identisch sind? | ||
| + | |||
| + | <math>H_2O</math> und <math>\left{P|P \notin \operatorname{Kurpfalz}\right}</math> helfen: <br /> | ||
| + | ::<math>A \subset B</math> bedeutet: Jedes Element von <math>A</math> gehört auch zu <math>B</math>. | ||
| + | ::<math>B \subset A</math> bedeutet: Jedes Element von <math>B</math> gehört auch zu <math>A</math>.<br /><br /> | ||
| + | Wir haben also zu zeigen, dass | ||
| + | #<math>E \in A \Rightarrow E \in B</math> und | ||
| + | #<math>E \in B \Rightarrow E \in A</math> gilt. | ||
| + | |||
| + | ===Ein Beispiel=== | ||
| + | ====Grundlegendes vorab==== | ||
| + | Wir gehen von folgenden Definitionen aus: | ||
| + | {{Definition|''Drachen''<br />Ein Viereck heißt ''Drachen'', wenn es ''zwei'' Paare von ''benachbarten'' Seiten hat, die zueinander kongruent sind.}} | ||
| + | {{Definition|''Parallelogramm''<br />Ein Viereck heißt ''Parallelogramm'', wenn es zwei ''Paare'' gegenüberliegender Seiten hat, die zueinander kongruent sind.}} | ||
| + | Unter <math>D^*</math> wollen wir die Menge aller Drachen verstehen, deren Diagonalen einander halbieren. | ||
| + | <math>P^*</math> sei die Menge aller Parallelogramme, deren Seiten alle kongruent zueinander sind. | ||
| + | |||
| + | Wir behaupten jetzt, dass <math>D^*=P^*</math> gilt.<br /> | ||
| + | ====Was ist zu beweisen?==== | ||
| + | |||
| + | # Wenn ein Viereck <math>V</math> ein Drachen ist, dessen Diagonalen einander halbieren, so ist <math>V</math> auch ein Parallelogramm, dessen Seiten alle kongruent zueinander sind. | ||
| + | # Wenn ein Viereck <math>V</math> ein Parallelogramm ist, dessen Seiten alle zueinander kongruent sind, dann ist <math>V</math> auch ein Drachen, dessen Diagonalen einander halbieren. | ||
| + | |||
| + | anders ausgedrückt: | ||
| + | |||
| + | # <math>V \in D^* \Rightarrow V \in P^*</math> | ||
| + | # <math>V \in P^* \Rightarrow V \in D^*</math> | ||
| + | |||
| + | oder zusammengefasst: | ||
| + | ::<math>V \in D^* \Leftrightarrow V \in P^*</math> | ||
| + | |||
| + | ====Die eigentlichen Beweise==== | ||
| + | =====Beweis 1===== | ||
| + | ======Vorbetrachtungen====== | ||
| + | Es sei <math>V=\overline{ABCD}</math> ein Drachen, dessen Diagonalen <math>\overline{AC}</math> und <math>\overline{BD}</math> sich im Punkt <math>M</math> schneiden mögen.<br /> | ||
| + | Voraussetzung: | ||
| + | ::(I) <math>\overline{AM} \tilde= \overline{MC}</math> und | ||
| + | ::(II) <math>\overline{BM} \tilde= \overline{MD}</math><br /> | ||
| + | Behauptung: | ||
| + | ::<math>\overline{AB} \tilde= \overline{BC} \tilde= \overline{CD} \tilde= \overline{DA}</math> | ||
| + | ======Der eigentliche Beweis====== | ||
| + | Versuchen Sie es selbst. Hinweis: zeigen Sie zunächst, dass im Drachen die Diagonalen senkrecht aufeinander stehen (kongruente Nebenwinkel sind rechte Winkel.) Dreieckskongruenzsätze helfen.<br /><br /> | ||
| + | '''Einschub''' | ||
| + | Numero6 hatte eine Verständnisfrage, der ich hier mal eine eigene Datei spendiere: [[Diagonalen im Drachen]] | ||
| + | |||
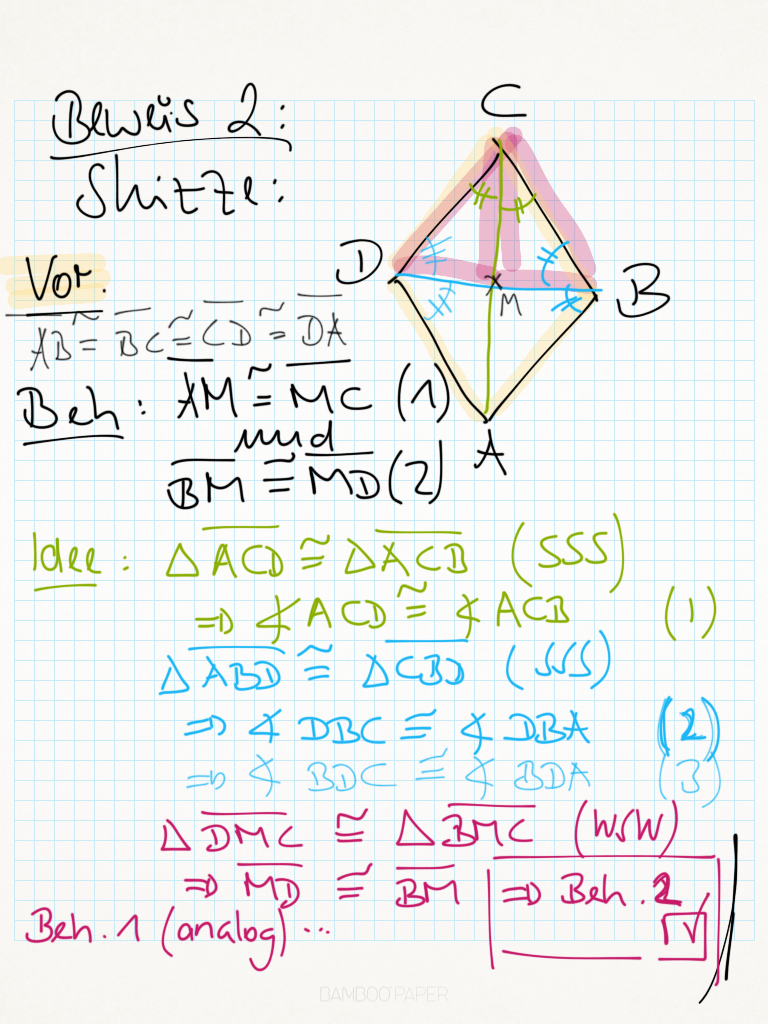
| + | =====Beweis 2===== | ||
| + | ======Vorbetrachtungen====== | ||
| + | Es sei <math>V=\overline{ABCD}</math> ein Parallelogramm, dessen Diagonalen sich im Punkt <math>M</math><br /> schneiden. | ||
| + | Voraussetzung: | ||
| + | ::<math>\overline{AB} \tilde= \overline{BC} \tilde= \overline{CD} \tilde= \overline{DA}</math><br /> | ||
| + | Behauptung:<br /> | ||
| + | ::(I) <math>\overline{AM} \tilde= \overline{MC}</math> und | ||
| + | ::(II) <math>\overline{BM} \tilde= \overline{MD}</math><br /> | ||
| + | ======Der eigentliche Beweis====== | ||
| + | Versuchen Sie es selbst. | ||
| + | |||
| + | Meine schnelle Beweisidee und ein Versuch das Bild in Geowiki einzubinden ;-)<br /> | ||
| + | [[Datei:SchnelleBeweis2Idee.PNG]]<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 22:03, 7. Jun. 2012 (CEST)<br /> | ||
| + | |||
| + | So kann es funktionieren.--[[Benutzer:*m.g.*|*m.g.*]] 08:00, 8. Jun. 2012 (CEST) | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 8. Juni 2012, 07:00 Uhr
Inhaltsverzeichnis |
Aufgabe 2.3
Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?
Lösungsvorschläge
ZigZag
- Dass die Schnittmenge C der Mengen A und B alle Elemente der Mengen A und B beinhaltet.Benutzer:Zigzag
Wurzel alias H2O
- A ist Teilmenge von B und B ist Teilmenge von A Dan ist A gleich B KeinKurpfälzer und --H2O 16:14, 30. Apr. 2012 (CEST)
TiCron
- Zwei Mengen sind identisch, wenn sie die selben Elemente enthalten. Kein Widerspruch zu H20 und KeinKurpfälzer.
Bemerkungen M.G.
Kommentar
Das ist soweit alles richtig, aber vielleicht noch nicht so wirklich hilfreich bezüglich des Führens von Beweisen.
Zunächst die Definition aus dem Skript:

Definition
Mengengleichheit
Zwei Mengen sind genau dann gleich, wenn sie aus denselben Elementen bestehen.
Diese Definition entspricht dem Beitrag von TiCron.
Auch in der Kurpfalz gilt jetzt das, was Team Fehler beim Parsen(Syntaxfehler): \left{ \operatorname{Wasser, nicht aus der Kurpfalz}\right}
formuliert:
Satz:
- Es seien
 und
und  zwei Mengen. Wenn
zwei Mengen. Wenn 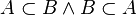 , dann
, dann 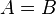 .
.
- Es seien
ZigZag drückt das so aus:
Satz:
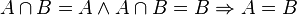 .
.
Beide Sätze könnten auch als Kriterium formuliert (gdw.) und somit als Definition verwendet werden.
Was muss ich aber konkret machen, wenn ich zeigen will, dass zwei Mengen  und
und  identisch sind?
identisch sind?
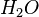 und Fehler beim Parsen(Syntaxfehler): \left{P|P \notin \operatorname{Kurpfalz}\right}
und Fehler beim Parsen(Syntaxfehler): \left{P|P \notin \operatorname{Kurpfalz}\right}
helfen:
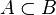 bedeutet: Jedes Element von
bedeutet: Jedes Element von  gehört auch zu
gehört auch zu  .
.
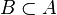 bedeutet: Jedes Element von
bedeutet: Jedes Element von  gehört auch zu
gehört auch zu  .
.
Wir haben also zu zeigen, dass
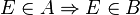 und
und
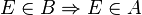 gilt.
gilt.
Ein Beispiel
Grundlegendes vorab
Wir gehen von folgenden Definitionen aus:
Definition
Drachen
Ein Viereck heißt Drachen, wenn es zwei Paare von benachbarten Seiten hat, die zueinander kongruent sind.
Definition
Parallelogramm
Ein Viereck heißt Parallelogramm, wenn es zwei Paare gegenüberliegender Seiten hat, die zueinander kongruent sind.
Unter 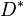 wollen wir die Menge aller Drachen verstehen, deren Diagonalen einander halbieren.
wollen wir die Menge aller Drachen verstehen, deren Diagonalen einander halbieren.
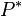 sei die Menge aller Parallelogramme, deren Seiten alle kongruent zueinander sind.
sei die Menge aller Parallelogramme, deren Seiten alle kongruent zueinander sind.
Wir behaupten jetzt, dass 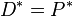 gilt.
gilt.
Was ist zu beweisen?
- Wenn ein Viereck
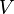 ein Drachen ist, dessen Diagonalen einander halbieren, so ist
ein Drachen ist, dessen Diagonalen einander halbieren, so ist 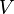 auch ein Parallelogramm, dessen Seiten alle kongruent zueinander sind.
auch ein Parallelogramm, dessen Seiten alle kongruent zueinander sind.
- Wenn ein Viereck
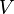 ein Parallelogramm ist, dessen Seiten alle zueinander kongruent sind, dann ist
ein Parallelogramm ist, dessen Seiten alle zueinander kongruent sind, dann ist 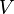 auch ein Drachen, dessen Diagonalen einander halbieren.
auch ein Drachen, dessen Diagonalen einander halbieren.
anders ausgedrückt:
oder zusammengefasst:
Die eigentlichen Beweise
Beweis 1
Vorbetrachtungen
Es sei 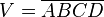 ein Drachen, dessen Diagonalen
ein Drachen, dessen Diagonalen  und
und 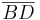 sich im Punkt
sich im Punkt  schneiden mögen.
schneiden mögen.
Voraussetzung:
- (I)
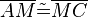 und
und
- (II)
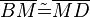
- (I)
Behauptung:
Der eigentliche Beweis
Versuchen Sie es selbst. Hinweis: zeigen Sie zunächst, dass im Drachen die Diagonalen senkrecht aufeinander stehen (kongruente Nebenwinkel sind rechte Winkel.) Dreieckskongruenzsätze helfen.
Einschub
Numero6 hatte eine Verständnisfrage, der ich hier mal eine eigene Datei spendiere: Diagonalen im Drachen
Beweis 2
Vorbetrachtungen
Es sei 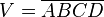 ein Parallelogramm, dessen Diagonalen sich im Punkt
ein Parallelogramm, dessen Diagonalen sich im Punkt 
schneiden.
Voraussetzung:
Behauptung:
- (I)
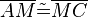 und
und
- (II)
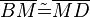
- (I)
Der eigentliche Beweis
Versuchen Sie es selbst.
Meine schnelle Beweisidee und ein Versuch das Bild in Geowiki einzubinden ;-)
--Tchu Tcha Tcha 22:03, 7. Jun. 2012 (CEST)
So kann es funktionieren.--*m.g.* 08:00, 8. Jun. 2012 (CEST)