Lösung von Zusatzaufgabe 2.5 neu (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 5) |
(→Aufgabe 5) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<br /> | <br /> | ||
| + | Da die Kontraposition bewiesenermaßen (s. Wahrheitstabelle) den selben Wahrheitsgehalt wie die Implikation hat, kann anstelle der Implikation auch die Kontraposition eines geometrischen Satzes bewiesen werden. | ||
| + | |||
| + | --[[Benutzer:*osterhase*|*osterhase*]] 20:10, 10. Jun. 2012 (CEST) | ||
| Zeile 42: | Zeile 45: | ||
--[[Benutzer:Goliath|Goliath]] 14:50, 29. Apr. 2012 (CEST)<br /> | --[[Benutzer:Goliath|Goliath]] 14:50, 29. Apr. 2012 (CEST)<br /> | ||
*So, ich habs mal geändert. Kannst es dir ja mal anschauen, wie das geht. --[[Benutzer:Andreas|Tutor Andreas]] 16:30, 29. Apr. 2012 (CEST) | *So, ich habs mal geändert. Kannst es dir ja mal anschauen, wie das geht. --[[Benutzer:Andreas|Tutor Andreas]] 16:30, 29. Apr. 2012 (CEST) | ||
| − | @ Andreas: Dankeschön. Werde mich mal einlesen. :-) | + | @ Andreas: Dankeschön. Werde mich mal einlesen. :-)--[[Benutzer:Goliath|Goliath]] 16:11, 2. Mai 2012 (CEST) |
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 10. Juni 2012, 19:10 Uhr
Aufgabe 5
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
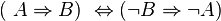
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Da die Kontraposition bewiesenermaßen (s. Wahrheitstabelle) den selben Wahrheitsgehalt wie die Implikation hat, kann anstelle der Implikation auch die Kontraposition eines geometrischen Satzes bewiesen werden.
--*osterhase* 20:10, 10. Jun. 2012 (CEST)
| A | B | 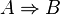
|
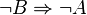
|
(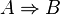 ) )  ( (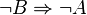 ) )
|
|---|---|---|---|---|
| w | w | w | w | w |
| w | f | f | f | w |
| f | w | w | w | w |
| f | f | w | w | w |
ich wusste leider nicht, wie man mathematische Formeln in eine Tabelle einfügt.
--Goliath 14:50, 29. Apr. 2012 (CEST)
- So, ich habs mal geändert. Kannst es dir ja mal anschauen, wie das geht. --Tutor Andreas 16:30, 29. Apr. 2012 (CEST)
@ Andreas: Dankeschön. Werde mich mal einlesen. :-)--Goliath 16:11, 2. Mai 2012 (CEST)

