Lösung von Aufg. 5.7P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 5.5 nicht wahr ist. | + | Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 5.5 nicht wahr ist.<br /><br /> |
| + | --[[Benutzer:Studentin|Studentin]] 08:46, 11. Mai 2012 (CEST)[[datei:Durchschnitt_punktmengen_konvex_.jpg ]]<br /> | ||
| + | |||
| + | Wie heißt den die Umkehrung?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:36, 22. Mai 2012 (CEST)<br /><br /> | ||
| + | implikation <math>a \rightarrow b</math>: <br /> | ||
| + | Der Durchschnitt zweier konvexer Punktmengen ist konvex<br /> | ||
| + | |||
| + | a: zwei konvexe punktmengen<br /> | ||
| + | b: durchschnitt ist konvex<br /> | ||
| + | |||
| + | unkehrung <math>b \rightarrow a</math>:<br /> | ||
| + | wenn der durchnitt zweier punktmengen konvex ist, sind die beiden mengen konvexe punktmengen<br />--[[Benutzer:Studentin|Studentin]] 19:33, 22. Mai 2012 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 22. Mai 2012, 18:33 Uhr
Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 5.5 nicht wahr ist.
--Studentin 08:46, 11. Mai 2012 (CEST)
Wie heißt den die Umkehrung?--Tutorin Anne 18:36, 22. Mai 2012 (CEST)
implikation 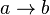 :
:
Der Durchschnitt zweier konvexer Punktmengen ist konvex
a: zwei konvexe punktmengen
b: durchschnitt ist konvex
unkehrung 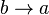 :
:
wenn der durchnitt zweier punktmengen konvex ist, sind die beiden mengen konvexe punktmengen
--Studentin 19:33, 22. Mai 2012 (CEST)

