Übung 7 (SoSe 12): Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Aufgabe | + | == Aufgabe 7.1 == |
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen? | Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen? | ||
| Zeile 11: | Zeile 11: | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 7.1_S (SoSe_12)]] |
<br/> | <br/> | ||
| − | == Aufgabe | + | == Aufgabe 7.2 == |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
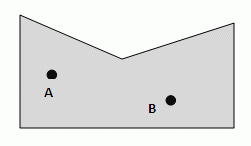
[[Bild:konvex02.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /> | [[Bild:konvex02.gif|links]]<br /><br /><br /><br /><br /><br /><br /><br /> | ||
Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die Figur konvex."<br /> | Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die Figur konvex."<br /> | ||
Wo liegt XYs Denkfehler?<br /> | Wo liegt XYs Denkfehler?<br /> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 7.2_S (SoSe_12)]] |
| − | == Aufgabe | + | == Aufgabe 7.3 == |
'''Satz: Der Durchschnitt zweier konvexer Punktmengen ist konvex.'''<br /><br /> | '''Satz: Der Durchschnitt zweier konvexer Punktmengen ist konvex.'''<br /><br /> | ||
a) Beweisen Sie den Satz.<br /> | a) Beweisen Sie den Satz.<br /> | ||
b) Wie lautet die Kontraposition?<br /> | b) Wie lautet die Kontraposition?<br /> | ||
c) Wie lautet die Umkehrung? Widerlegen Sie die Umkehrung durch eine Skizze.<br /> | c) Wie lautet die Umkehrung? Widerlegen Sie die Umkehrung durch eine Skizze.<br /> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 7.3_S (SoSe_12)]] |
| − | == Aufgabe | + | == Aufgabe 7.4 == |
Ergänzen Sie die Definition für offene Halbebenen <math>\ gQ^{+} </math> und <math>\ gQ^{-} </math><br /> | Ergänzen Sie die Definition für offene Halbebenen <math>\ gQ^{+} </math> und <math>\ gQ^{-} </math><br /> | ||
("Offen" bedeutet hier: Die Halbebene '''ohne''' die Gerade, die die Ebene teilt).<br /> | ("Offen" bedeutet hier: Die Halbebene '''ohne''' die Gerade, die die Ebene teilt).<br /> | ||
| Zeile 47: | Zeile 34: | ||
<math>\ gQ^{+} := \{P|...\} </math><br /> | <math>\ gQ^{+} := \{P|...\} </math><br /> | ||
<math>\ gQ^{-} := \{P|...\}</math> <br /> | <math>\ gQ^{-} := \{P|...\}</math> <br /> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 7.4_S (SoSe_12)]] |
| − | == Aufgabe | + | == Aufgabe 7.5 == |
Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte A, B und C in einer Ebene E. Außerdem sei eine Gerade g Teilmenge von E, wobei keiner der Punkte A, B und C auf g liegen möge.<br /> | Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte A, B und C in einer Ebene E. Außerdem sei eine Gerade g Teilmenge von E, wobei keiner der Punkte A, B und C auf g liegen möge.<br /> | ||
Es gilt folgender Zusammenhang:<br /> | Es gilt folgender Zusammenhang:<br /> | ||
| Zeile 58: | Zeile 45: | ||
b) Beweisen Sie den oben genannten Zusammenhang. | b) Beweisen Sie den oben genannten Zusammenhang. | ||
| − | <br />[[Lösung von Aufgabe | + | <br />[[Lösung von Aufgabe 7.5_S (SoSe_12)]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 31. Mai 2012, 16:01 Uhr
Inhaltsverzeichnis |
Aufgabe 7.1
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
a)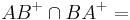 
b)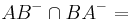 
c) 
geschnitten mit dem Kreis um 
durch 
=
d)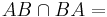
Lösung von Aufgabe 7.1_S (SoSe_12)
Aufgabe 7.2
Student XY argumentiert: "Weil 
komplett innerhalb der Punktmenge liegt, ist die Figur konvex."
Wo liegt XYs Denkfehler?
Lösung von Aufgabe 7.2_S (SoSe_12)
Aufgabe 7.3
Satz: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
a) Beweisen Sie den Satz.
b) Wie lautet die Kontraposition?
c) Wie lautet die Umkehrung? Widerlegen Sie die Umkehrung durch eine Skizze.
Lösung von Aufgabe 7.3_S (SoSe_12)
Aufgabe 7.4
Ergänzen Sie die Definition für offene Halbebenen 
und 
("Offen" bedeutet hier: Die Halbebene ohne die Gerade, die die Ebene teilt).
Definition (offene Halbebene):
- Es sei E eine Ebene, in der die Gerade g und der Punkt Q liegen mögen. Q gehöre nicht zu g. Unter den offenen Teilmengen und bezüglich der Trägergeraden g versteht man die folgenden Teilmengen von E:
- Es sei E eine Ebene, in der die Gerade g und der Punkt Q liegen mögen. Q gehöre nicht zu g. Unter den offenen Teilmengen
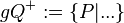
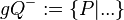
Lösung von Aufgabe 7.4_S (SoSe_12)
Aufgabe 7.5
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Außerdem sei eine Gerade g Teilmenge von E, wobei keiner der Punkte A, B und C auf g liegen möge.
Es gilt folgender Zusammenhang:
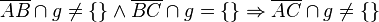
a) Fertigen Sie eine Skizze an, aus der der oben genannte Zusammenhang ersichtlich wird.
b) Beweisen Sie den oben genannten Zusammenhang.
