Lösung von Aufgabe 6.1 S (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Halbgerade AB-) |
(→Lösung von Nummero6/Tchu Tcha Tcha:) |
||
| (27 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 99: | Zeile 99: | ||
Länge einer Strecke <math>\overline{AB}</math> in formaler Schreibweise:<math>\left|\overline{AB}\right|</math>.<br /> | Länge einer Strecke <math>\overline{AB}</math> in formaler Schreibweise:<math>\left|\overline{AB}\right|</math>.<br /> | ||
Definition: <math>\left|\overline{AB}\right|:=\left|AB\right|</math> | Definition: <math>\left|\overline{AB}\right|:=\left|AB\right|</math> | ||
| + | |||
| + | ====Zwischenfrage von Snooth==== | ||
| + | Ich hätte gerne gewusst, ob man den Begriff "Endpunkt" an dieser Stelle undefiniert verwenden darf? | ||
| + | --[[Benutzer:Snooth|Snooth]] 13:54, 16. Jun. 2012 (CEST) | ||
| + | =====Antwort M.G.===== | ||
| + | Der Begriff Endpunkt einer Strecke sollte vorab definiert sein. In der Regel erledigt man das gleich in der Definition des Begriffs Strecke. | ||
| + | {{Definition|(Strecke)<br />Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Unter der Strecke <math>\overline{AB}</math> versteht man die Menge aller Punkte <math>P</math>, die zwischen den Punkten <math>A</math> und <math>B</math> liegen, vereinigt mit der Menge, die aus den Punkten <math>A</math> und <math>B</math> besteht. Die Punkte <math>A</math> und <math>B</math> heißen Endpunkte der Strecke <math>\overline{AB}</math>.}} | ||
| + | --[[Benutzer:*m.g.*|*m.g.*]] 16:27, 16. Jun. 2012 (CEST) | ||
| + | Hab grad noch mal nachgesehen. In der Definition II.3 (offene Strecke, Strecke, Endpunkte einer Strecke) ist alles definiert.--[[Benutzer:*m.g.*|*m.g.*]] 16:46, 16. Jun. 2012 (CEST) | ||
====Halbgerade AB<sup>+</sup>==== | ====Halbgerade AB<sup>+</sup>==== | ||
passt | passt | ||
| Zeile 105: | Zeile 114: | ||
Versuchen Sie es noch mal: | Versuchen Sie es noch mal: | ||
| − | Defintion: ( | + | Defintion: (Halbgerade bzw. Strahl <math>AB^-</math>)<br /> |
:::<math>AB^-:=\left{ P|...\right} \cup \left{ ...\right}</math>. | :::<math>AB^-:=\left{ P|...\right} \cup \left{ ...\right}</math>. | ||
| + | <br />'''Versuch Def. (geschlossene Halbgerade bzw. Strahl <math>AB^-</math>) Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| + | :::<math>AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup \left{A\right}</math>.<br /> | ||
| + | Unter der Halbgeraden <math>AB^-</math> versteht man die Punktmenge A vereinigt mit der Menge aller Punkte P für die gilt: ZW (P,A,B).<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:50, 9. Jun. 2012 (CEST) | ||
| + | Bemerkung M.G.: | ||
| + | :Inhaltlich ist das richtig. Von der Syntax stimmt es mit der Menge <math>\left{A\right}</math> noch nicht ganz. Wenn Sie ".. die Punktmenge <math>A</math> ... " schreiben, dann bedeutet das: Die Menge von Punktmengen mit der Bezeichnung <math>A</math>. Sie meinen jedoch die Menge, die nur aus dem Punkt <math>A</math> besteht. Das ist ein Unterschied. | ||
| + | |||
| + | Ihre Formulierung korrekt: | ||
| + | ::Unter der Halbgeraden <math>AB^-</math> versteht man die Punktmenge, die aus dem Punkt <math>A</math> besteht, vereinigt mit der Menge aller Punkte <math>P</math> für die gilt: <math>\operatorname Zw (P,A,B)</math>. --[[Benutzer:*m.g.*|*m.g.*]] 16:36, 16. Jun. 2012 (CEST) | ||
| + | <br /> | ||
| + | OK, danke. Dann müsste ich es also so schreiben, damit die Syntax stimmt?? | ||
| + | :::<math>AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup A</math>.<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:04, 16. Jun. 2012 (CEST)<br /> | ||
| + | <br /> | ||
| + | Nein, oben die formale Schreibweise mit Mengenklammern um A war richtig. Es ging Herrn Gieding nur um Ihre ausformulierte Version.<br />--[[Benutzer:Buchner|Buchner]] 10:14, 17. Jun. 2012 (CEST)<br /> | ||
| + | |||
| + | '''Endversion Nummero6/Tchu Tcha Tcha'''<br /> | ||
| + | <math>AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup \left{A\right}</math><br /> | ||
| + | Unter der Halbgeraden <math>AB^-</math> versteht man die Punktmenge, die aus dem Punkt <math>A</math> besteht, vereinigt mit der Menge aller Punkte <math>P</math> für die gilt: <math>\operatorname Zw (P,A,B)</math>.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:57, 17. Jun. 2012 (CEST) | ||
| + | <br /> | ||
| + | Perfekt.--[[Benutzer:Buchner|Buchner]] 17:40, 17. Jun. 2012 (CEST) | ||
====sonstige Bemerkungen==== | ====sonstige Bemerkungen==== | ||
| Zeile 115: | Zeile 145: | ||
Versuchen Sie es: | Versuchen Sie es: | ||
| − | Definition S: (Punkt einer Strecke <math>\overline{AB}</math> <br /> | + | Definition S: (Punkt einer Strecke <math>\overline{AB}</math>) <br /> |
::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Ein Punkt <math>P</math> ist ein Punkt der Strecke <math>\overline{AB}</math>, wenn ... . | ::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Ein Punkt <math>P</math> ist ein Punkt der Strecke <math>\overline{AB}</math>, wenn ... . | ||
| Zeile 124: | Zeile 154: | ||
::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Unter der Halbgeraden <math>AB^-</math> versteht man die Menge der Punkte der Geraden <math>AB</math>, die nicht ... . | ::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Unter der Halbgeraden <math>AB^-</math> versteht man die Menge der Punkte der Geraden <math>AB</math>, die nicht ... . | ||
| − | Hinweis zur Definition HG<sup>-</sup>: Auf oHG<sup>+</sup> darf zurückgegriffen werden. | + | Hinweis zur Definition HG<sup>-</sup>: Auf oHG<sup>+</sup> darf zurückgegriffen werden.<br /> |
| + | <br /> | ||
| + | ''' | ||
| + | |||
| + | == Lösung von Nummero6/Tchu Tcha Tcha: == | ||
| + | ''' | ||
| + | Definition S: (Punkt einer Strecke <math>\overline{AB}</math>) <br /> | ||
| + | ::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Ein Punkt <math>P</math> ist ein Punkt der Strecke <math>\overline{AB}</math>, wenn <math>P</math>=<math>A</math>oder<math>P</math>=<math>B</math>oder<math>\operatorname Zw (A, P, B)</math> . | ||
| + | |||
| + | Definition oHG<sup>+</sup>: (offene Halbgerade <math>AB^+</math>)<br /> | ||
| + | ::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Unter der offenen Halbgeraden <math>AB^+</math> versteht man die Menge aller Punkte <math>P</math> von der Geraden <math>AB</math>, für die nicht gilt: <math>\operatorname \ Zw (P, A, B) \cup A </math> . | ||
| + | |||
| + | Definition HG<sup>-</sup>: (Halbgerade <math>AB^-</math>)<br /> | ||
| + | ::Es seien <math>A</math> und <math>B</math> zwei verschiedene Punkte. Unter der Halbgeraden <math>AB^-</math> versteht man die Menge der Punkte der Geraden <math>AB</math>, die nicht zur Menge der offenen Halbgeraden <math>AB^+</math>gehören.<br /> | ||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 14:10, 9. Jun. 2012 (CEST) | ||
====noch ein paar Bemerkungen==== | ====noch ein paar Bemerkungen==== | ||
| − | Begriffe versteht man erst, wenn man | + | Begriffe versteht man erst, wenn man sie aus "verschiedenen Blickwinkeln" betrachtet. Das ist das Wichtigste, was Sie hier für Ihre spätere Tätigkeit als Lehrer mitnehmen sollen.<br /> |
--[[Benutzer:*m.g.*|*m.g.*]] 06:14, 9. Jun. 2012 (CEST) | --[[Benutzer:*m.g.*|*m.g.*]] 06:14, 9. Jun. 2012 (CEST) | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 1. Juli 2012, 13:40 Uhr
Aufgabe 6.1
Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade  und die Halbgerade
und die Halbgerade  . Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
Lösung von Monsta
Strecke:
Es seien A und B zwei verschiedene Punkte auf einer Geraden g. Alle Punkte die auf dieser Geraden zwischen A und B liegen, zusammen mit den beiden Punkten selbst, bilden die Strecke AB.
Halbgerade AB+
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von A aus hinter B liegen vereinigt, dann erhält man die Halbgerade AB+.
Halbgerade AB-
Es seien A und B zwei verschiedene Punkte. Wenn man die Strecke AB und alle Punkte P, die mit AB kollinear sind und von B aus hinter A liegen vereinigt, dann erhält man die Halbgerade AB-.
--Monsta 22:41, 4. Jun. 2012 (CEST)
Anmerkungen von Buchner zu Monstas Definitionen
Zur Definition Strecke: Die Definition ist korrekt- allerdings brauchen Sie die Gerade g nicht zu nennen. Die Zwischenrealtion beinhaltet schon, dass alle Punkte kollinear sein müssen.
Zur Definition  : Von der Idee absolut richtig. Allerdings ist "hinter B liegen" informell. Versuchen Sie es mal mit der Zwischenrealtion auszudrücken!
: Von der Idee absolut richtig. Allerdings ist "hinter B liegen" informell. Versuchen Sie es mal mit der Zwischenrealtion auszudrücken!
Zur Definition 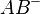 : Achtung: Strecke
: Achtung: Strecke  gehört nicht dazu!
gehört nicht dazu!
--Buchner 12:20, 6. Jun. 2012 (CEST)
Lösung von Mahe84
Def. Strecke:
Eine Strecke AB (mit "überstrich") wird die Vereinigungsmenge der offene Strecke (AB) mit den Punkten A und B bezeichnet. oder AB (mit "übertrich") : = (AB) u {A,B}
Länge einer Strecke:
Der Abstand I AB I der Strecke AB (mit "überstrich") wird als Länge der Strecke AB bezeichnet.
Halbgerade AB+:
Existiert für die Strecke AB (mit "überstrich") ein Punkt, für den entweder Zw (ABP), Zw (APB) oder identisch mit B gilt, wird die Strecke Halbgerade AB+ genannt.
Halbgerade AB-:
Existiert für die Strecke AB (mit "überstrich") ein Punkt, für den Zw (PAB) gilt, wird die Strecke Halbgerade AB- genannt. --Mahe84 16:07, 7. Jun. 2012 (CEST)
Bemerkungen von M.G. zu den Definitionen von Mahe84
Vorbemerkung
Sie sind auf dem richtigen Weg. Nur wenn man es probiert, die Begriffe aus eigener Kraft zu verbalisieren wird sich Erfolg einstellen. Kleine Unvollkommenheiten sind dabei notwendig, um Vollkommenheit zu erreichen. (s. hierzu meine Bemerkungen von heute in der Datei Selbstverteidigung und mentales Training (Veranstaltung vom 4. Juni)
Lassen Sie sich bitte nicht entmutigen und versuchen Sie die kleinen "Unvollkommenheiten" auszuräumen. Ich weiß, es bedarf einer hohen Frusttoleranz, aber eine solche müssen Sie ja später auch bei Ihren Schülern entwickeln.
Definition Strecke
Prinzipiell ist Ihre Definition richtig. Vom Ausdruck her lässt sie zu wünschen übrig.Ich lass mal einiges weg, um die sprachlichen Ungereimtheiten zu verdeutlichen: Eine Strecke wird die Vereinigungsmenge bezeichnet. Da stimmt was nicht. Ich nehme an, reine Flüchtigkeit. Man liest sich das Ganze zwar abschließend durch, liest jedoch nicht wirklich sondern das was man lesen möchte. Mit einigem zeitlichen Abstand fragt man sich verständnislos, was man da geschrieben hat.
Die Sache mit der Vereingungsmenge geht dann jedoch auch aus der Sicht der mathematischen Syntax schief: Sie wollen die offene Strecke  mit den Punkten
mit den Punkten  und
und  vereinigen. Eine offene Strecke ist eine Punktmenge. Dies können Sie nur mit einer Menge von Punkten vereinigen. Dementsprechend müssen die beiden Punkte als Menge von Punkten betrachtet werden.
vereinigen. Eine offene Strecke ist eine Punktmenge. Dies können Sie nur mit einer Menge von Punkten vereinigen. Dementsprechend müssen die beiden Punkte als Menge von Punkten betrachtet werden.
Kleine Hilfe: Ich bereite die Definition in Ihrem Sinne schon mal mit Tex-Tags vor:
Strecke: ...Strecke  wird die Vereinigungsmenge der offenen Strecke
wird die Vereinigungsmenge der offenen Strecke  mit der Menge, die aus den Punkten
mit der Menge, die aus den Punkten  und
und  besteht, bezeichnet.
besteht, bezeichnet.
Definition Länge einer Strecke
Die Länge einer Strecke ist der Abstand, den ihre Endpunkte zueinander haben. Das haben Sie richtig erkannt. Die Ungereimtheit liegt wieder im Ausdruck aus Sicht der deutschen Sprache:
Wenn Sie schreiben: Der Abstand 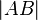 dann ist der Abstand der beiden Punkte zueinander gemeint. Damit ist der Abstand der beiden Punkte den beiden Punkten zuzuordnen. Sie schreiben jedoch: Der Abstand
dann ist der Abstand der beiden Punkte zueinander gemeint. Damit ist der Abstand der beiden Punkte den beiden Punkten zuzuordnen. Sie schreiben jedoch: Der Abstand 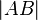 der Strecke
der Strecke  ... . Das passt so nicht. Ich verdeutliche das noch mal auf andere Art und Weise. Der Abstand zweier Punkte ist eine Zahl, die wir hier mal mit
... . Das passt so nicht. Ich verdeutliche das noch mal auf andere Art und Weise. Der Abstand zweier Punkte ist eine Zahl, die wir hier mal mit  bezeichnen wollen. Unter Verwendung dieser Zahl
bezeichnen wollen. Unter Verwendung dieser Zahl  würde Ihre Definition wie folgt beginnen:
würde Ihre Definition wie folgt beginnen:
Es sei  der Abstand der beiden Punkte
der Abstand der beiden Punkte  und
und  . Die Zahl
. Die Zahl  der Strecke
der Strecke  ...
...
Ich bereite die korrekte Schreibweise für Sie wieder vor:
Länge einer Strecke: Der Abstand 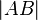 der ... der Strecke
der ... der Strecke  wird Länge von
wird Länge von  genannt.
genannt.
Definition Halbgerade  und
und 
Hier geht es richtig daneben. Zur Verdeutlichung das es so nicht geht, hier quasi die Quintessenz Ihrer Definitionen:
Definition Halbgerade:
- Gilt für eine Strecke eine gewisse Existenzaussage, dann ist die Strecke eine Halbgerade.
Ergo: Jede Halbgerade ist eine Strecke.
Damit werden die Mathematiker nicht einverstanden sein.
Hilfe: Eine Halbgerade ist eine Menge von Punkten.
Halbgerade  : Unter der Halbgeraden
: Unter der Halbgeraden  versteht man die Menge der Punkte der Strecke
versteht man die Menge der Punkte der Strecke  vereinigt mit ... .
vereinigt mit ... .
Korrekturen von Mahe84
Okay, vielen, vielen Dank für Ihre ausführliche Erläuterung, ich hoffe ich habe es jetzt verstanden!
Def. Strecke, ist klar, mit ein "wenig zeitlichem Abstand" ist es auch mir aufgefallen ...
Def. Länge einer Strecke:
Der Abstand 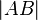 der beiden Punkte A und B der Strecke
der beiden Punkte A und B der Strecke  wird Länge von
wird Länge von  genannt.
genannt.
Def. Halbgerade:
Unter der Halbgeraden  versteht man die Menge der Punkte der Strecke
versteht man die Menge der Punkte der Strecke  vereinigt mit der Menge aller Punkte P für die gilt: Zw(A,B,P).
vereinigt mit der Menge aller Punkte P für die gilt: Zw(A,B,P).
Unter der Halbgeraden  versteht man die Menge der Punkte der Stercke
versteht man die Menge der Punkte der Stercke  vereinigt mit der Menge aller Punkte P für die gilt: ZW (P,A,B).
vereinigt mit der Menge aller Punkte P für die gilt: ZW (P,A,B).
Bemerkungen M.G. zu den Korrekturen
Länge
So passt es. Aus rein didaktischer Sicht könnte man noch erwähnen, dass  und
und  die Endpunkte der Strecke sind:
die Endpunkte der Strecke sind:
Der Abstand 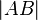 der Endpunkte
der Endpunkte  und
und  der Strecke
der Strecke  wird Länge von
wird Länge von  genannt.
genannt.
Oder:
Der Abstand der Endpunkte einer Strecke wird Länge dieser Strecke genannt.
Formal:
Länge einer Strecke  in formaler Schreibweise:
in formaler Schreibweise: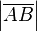 .
.
Definition: 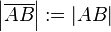
Zwischenfrage von Snooth
Ich hätte gerne gewusst, ob man den Begriff "Endpunkt" an dieser Stelle undefiniert verwenden darf?
--Snooth 13:54, 16. Jun. 2012 (CEST)
Antwort M.G.
Der Begriff Endpunkt einer Strecke sollte vorab definiert sein. In der Regel erledigt man das gleich in der Definition des Begriffs Strecke.
Definition
(Strecke)
Es seien  und
und  zwei verschiedene Punkte. Unter der Strecke
zwei verschiedene Punkte. Unter der Strecke  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  , die zwischen den Punkten
, die zwischen den Punkten  und
und  liegen, vereinigt mit der Menge, die aus den Punkten
liegen, vereinigt mit der Menge, die aus den Punkten  und
und  besteht. Die Punkte
besteht. Die Punkte  und
und  heißen Endpunkte der Strecke
heißen Endpunkte der Strecke  .
.
--*m.g.* 16:27, 16. Jun. 2012 (CEST) Hab grad noch mal nachgesehen. In der Definition II.3 (offene Strecke, Strecke, Endpunkte einer Strecke) ist alles definiert.--*m.g.* 16:46, 16. Jun. 2012 (CEST)
Halbgerade AB+
passt
Halbgerade AB-
 und
und  haben genau einen Punkt gemeinsam, nämlich den Anfangspunkt
haben genau einen Punkt gemeinsam, nämlich den Anfangspunkt  . Die Strecke
. Die Strecke  gehört nur zu
gehört nur zu  .
.
Versuchen Sie es noch mal:
Defintion: (Halbgerade bzw. Strahl  )
)
- Fehler beim Parsen(Syntaxfehler): AB^-:=\left{ P|...\right} \cup \left{ ...\right}
.
Versuch Def. (geschlossene Halbgerade bzw. Strahl  ) Nummero6/Tchu Tcha Tcha:
) Nummero6/Tchu Tcha Tcha:
- Fehler beim Parsen(Syntaxfehler): AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup \left{A\right}
.
Unter der Halbgeraden  versteht man die Punktmenge A vereinigt mit der Menge aller Punkte P für die gilt: ZW (P,A,B).
versteht man die Punktmenge A vereinigt mit der Menge aller Punkte P für die gilt: ZW (P,A,B).
--Tchu Tcha Tcha 13:50, 9. Jun. 2012 (CEST)
Bemerkung M.G.:
- Inhaltlich ist das richtig. Von der Syntax stimmt es mit der Menge Fehler beim Parsen(Syntaxfehler): \left{A\right}
noch nicht ganz. Wenn Sie ".. die Punktmenge... " schreiben, dann bedeutet das: Die Menge von Punktmengen mit der Bezeichnung
. Sie meinen jedoch die Menge, die nur aus dem Punkt
besteht. Das ist ein Unterschied.
Ihre Formulierung korrekt:
- Unter der Halbgeraden
 versteht man die Punktmenge, die aus dem Punkt
versteht man die Punktmenge, die aus dem Punkt  besteht, vereinigt mit der Menge aller Punkte
besteht, vereinigt mit der Menge aller Punkte  für die gilt:
für die gilt: 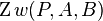 . --*m.g.* 16:36, 16. Jun. 2012 (CEST)
. --*m.g.* 16:36, 16. Jun. 2012 (CEST)
- Unter der Halbgeraden
OK, danke. Dann müsste ich es also so schreiben, damit die Syntax stimmt??
- Fehler beim Parsen(Syntaxfehler): AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup A
.
--Tchu Tcha Tcha 21:04, 16. Jun. 2012 (CEST)
Nein, oben die formale Schreibweise mit Mengenklammern um A war richtig. Es ging Herrn Gieding nur um Ihre ausformulierte Version.
--Buchner 10:14, 17. Jun. 2012 (CEST)
Endversion Nummero6/Tchu Tcha Tcha
Fehler beim Parsen(Syntaxfehler): AB^-:=\left{ P|\operatorname Zw (P, A, B)} \cup \left{A\right}
Unter der Halbgeraden  versteht man die Punktmenge, die aus dem Punkt
versteht man die Punktmenge, die aus dem Punkt  besteht, vereinigt mit der Menge aller Punkte
besteht, vereinigt mit der Menge aller Punkte  für die gilt:
für die gilt: 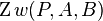 .
.
--Tchu Tcha Tcha 12:57, 17. Jun. 2012 (CEST)
Perfekt.--Buchner 17:40, 17. Jun. 2012 (CEST)
sonstige Bemerkungen
Schön, dass Sie dran geblieben sind. Versuchen Sie weiter zu analysieren, wo Ihre persönlichen Fehlerquellen liegen. Ich wette, die Sache mit der Halbgeraden  ist Ihnen absolut klar. Ihre letzte Definition war ein "Schnellschuss", bei dem Sie kurzerhand, ohne das Ganze noch einmal genau zu hinterfragen, das Schema von Halbgerade
ist Ihnen absolut klar. Ihre letzte Definition war ein "Schnellschuss", bei dem Sie kurzerhand, ohne das Ganze noch einmal genau zu hinterfragen, das Schema von Halbgerade  verwendet haben. Was lernen wir: Immer wieder die eigenen Überlegungen hinterfragen. Das ist es dann auch, was Sie später Ihren Schülern mit auf den Weg geben werden.
verwendet haben. Was lernen wir: Immer wieder die eigenen Überlegungen hinterfragen. Das ist es dann auch, was Sie später Ihren Schülern mit auf den Weg geben werden.
zur weiteren Übung
Richtig verstanden haben Sie die Dinge erst, wenn Sie jetzt die Definitionen bzw. Sachverhalte noch einmal anders formulieren können.
Versuchen Sie es:
Definition S: (Punkt einer Strecke  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Ein Punkt
zwei verschiedene Punkte. Ein Punkt  ist ein Punkt der Strecke
ist ein Punkt der Strecke  , wenn ... .
, wenn ... .
- Es seien
Definition oHG+: (offene Halbgerade  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Unter der offenen Halbgeraden
zwei verschiedene Punkte. Unter der offenen Halbgeraden  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  von ..., für die nicht gilt: ... .
von ..., für die nicht gilt: ... .
- Es seien
Definition HG-: (Halbgerade  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Unter der Halbgeraden
zwei verschiedene Punkte. Unter der Halbgeraden  versteht man die Menge der Punkte der Geraden
versteht man die Menge der Punkte der Geraden  , die nicht ... .
, die nicht ... .
- Es seien
Hinweis zur Definition HG-: Auf oHG+ darf zurückgegriffen werden.
Lösung von Nummero6/Tchu Tcha Tcha:
Definition S: (Punkt einer Strecke  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Ein Punkt
zwei verschiedene Punkte. Ein Punkt  ist ein Punkt der Strecke
ist ein Punkt der Strecke  , wenn
, wenn  =
= oder
oder =
= oder
oder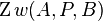 .
.
- Es seien
Definition oHG+: (offene Halbgerade  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Unter der offenen Halbgeraden
zwei verschiedene Punkte. Unter der offenen Halbgeraden  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  von der Geraden
von der Geraden  , für die nicht gilt:
, für die nicht gilt: 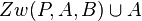 .
.
- Es seien
Definition HG-: (Halbgerade  )
)
- Es seien
 und
und  zwei verschiedene Punkte. Unter der Halbgeraden
zwei verschiedene Punkte. Unter der Halbgeraden  versteht man die Menge der Punkte der Geraden
versteht man die Menge der Punkte der Geraden  , die nicht zur Menge der offenen Halbgeraden
, die nicht zur Menge der offenen Halbgeraden  gehören.
gehören.
- Es seien
--Tchu Tcha Tcha 14:10, 9. Jun. 2012 (CEST)
noch ein paar Bemerkungen
Begriffe versteht man erst, wenn man sie aus "verschiedenen Blickwinkeln" betrachtet. Das ist das Wichtigste, was Sie hier für Ihre spätere Tätigkeit als Lehrer mitnehmen sollen.
--*m.g.* 06:14, 9. Jun. 2012 (CEST)

