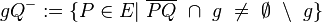Lösung von Aufgabe 7.4 S (SoSe 12): Unterschied zwischen den Versionen
Nemo81 (Diskussion | Beiträge) |
|||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
gQ<sup>-</sup> muss glaube ich noch "geschnitten mit nicht g" hinter der Klammer angehängt werden, um die Gerade auszuschließen. --[[Benutzer:Butterbrot|Butterbrot]] 14:23, 12. Jun. 2012 (CEST)<br /> | gQ<sup>-</sup> muss glaube ich noch "geschnitten mit nicht g" hinter der Klammer angehängt werden, um die Gerade auszuschließen. --[[Benutzer:Butterbrot|Butterbrot]] 14:23, 12. Jun. 2012 (CEST)<br /> | ||
| + | *Das stimmt, denn g gehört ja nicht zur offenen Halbebene gQ<sup>+</sup> und deshalb muss die Gerade aus der Menge ausgeschlossen werden.--[[Benutzer:Andreas|Tutor Andreas]] 16:32, 21. Jun. 2012 (CEST) | ||
'''weiterer ausformulierter Definitionsversuch von Nummero6/Tchu Tcha Tcha:'''<br /> | '''weiterer ausformulierter Definitionsversuch von Nummero6/Tchu Tcha Tcha:'''<br /> | ||
| − | <math>\ gQ^{+}</math>(offen): Alle Punkte der Ebene E, die zu Q bezüglich g auf derselben Ebene liegen und die nicht zur Geraden g gehören nennt man offene Halbebene <math>\ gQ^{+}</math>.<br /> | + | <math>\ gQ^{+}</math>(offen): Alle Punkte der Ebene E, die <s>zu</s> '''mit''' Q bezüglich g auf derselben '''Halb'''Ebene liegen und die nicht zur Geraden g gehören, nennt man offene Halbebene <math>\ gQ^{+}</math>.<br /> |
| − | <math>\ gQ^{-}</math>(offen): Alle Punkte der Ebene E, die zu Q bezüglich g auf der | + | <math>\ gQ^{-}</math>(offen): Alle Punkte der Ebene E, die <s>zu</s> '''nicht mit''' Q bezüglich g auf der selben '''Halb'''Ebene liegen und die nicht zur Geraden g gehören, nennt man offene Halbebene <math>\ gQ^{-}</math>.<br /> |
| − | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 16:39, 12. Jun. 2012 (CEST) | + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 16:39, 12. Jun. 2012 (CEST)<br /> |
| + | *Ich habe noch ein wenig verbessert und das habe ich '''fett''' geschrieben.--[[Benutzer:Andreas|Tutor Andreas]] 16:32, 21. Jun. 2012 (CEST) | ||
gQ+= (P: PQ n g = ( )) | gQ+= (P: PQ n g = ( )) | ||
| + | |||
gQ-= (P: PQ n g = (S)/g) | gQ-= (P: PQ n g = (S)/g) | ||
| − | --[[Benutzer:Nemo81|Nemo81]] 15:34, 13. Jun. 2012 (CEST) | + | --[[Benutzer:Nemo81|Nemo81]] 15:34, 13. Jun. 2012 (CEST)<br /> |
| + | *Da es sich um Mengen handelt, muss das ganze in geschweifte Klammern gesetzt werden. Ich habe es nochmal umgeschrieben. --[[Benutzer:Andreas|Tutor Andreas]] 16:35, 21. Jun. 2012 (CEST) | ||
| + | offene Halbebene <math>gQ^{+} := \{P \in E|\ \overline{PQ}\ \cap\ g\ =\ \empty \}</math><br /> | ||
| + | offene Halbebene <math>gQ^{-} := \{P \in E|\ \overline{PQ}\ \cap\ g\ \neq\ \empty\ \setminus \ g \}</math> | ||
Aktuelle Version vom 1. Juli 2012, 16:22 Uhr
--KeinKurpfälzer 17:23, 11. Jun. 2012 (CEST)
So würde ich es auch schreiben, außer bei
gQ- muss glaube ich noch "geschnitten mit nicht g" hinter der Klammer angehängt werden, um die Gerade auszuschließen. --Butterbrot 14:23, 12. Jun. 2012 (CEST)
- Das stimmt, denn g gehört ja nicht zur offenen Halbebene gQ+ und deshalb muss die Gerade aus der Menge ausgeschlossen werden.--Tutor Andreas 16:32, 21. Jun. 2012 (CEST)
weiterer ausformulierter Definitionsversuch von Nummero6/Tchu Tcha Tcha:
(offen): Alle Punkte der Ebene E, die zu mit Q bezüglich g auf derselben HalbEbene liegen und die nicht zur Geraden g gehören, nennt man offene Halbebene .
(offen): Alle Punkte der Ebene E, die zu nicht mit Q bezüglich g auf der selben HalbEbene liegen und die nicht zur Geraden g gehören, nennt man offene Halbebene .
--Tchu Tcha Tcha 16:39, 12. Jun. 2012 (CEST)
- Ich habe noch ein wenig verbessert und das habe ich fett geschrieben.--Tutor Andreas 16:32, 21. Jun. 2012 (CEST)
gQ+= (P: PQ n g = ( ))
gQ-= (P: PQ n g = (S)/g)
--Nemo81 15:34, 13. Jun. 2012 (CEST)
- Da es sich um Mengen handelt, muss das ganze in geschweifte Klammern gesetzt werden. Ich habe es nochmal umgeschrieben. --Tutor Andreas 16:35, 21. Jun. 2012 (CEST)
offene Halbebene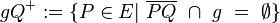 
offene Halbebene 
