Lösung von Aufgabe 7.5 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Nemo81 (Diskussion | Beiträge) |
(→Lösungsvorschlag Nemo81) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
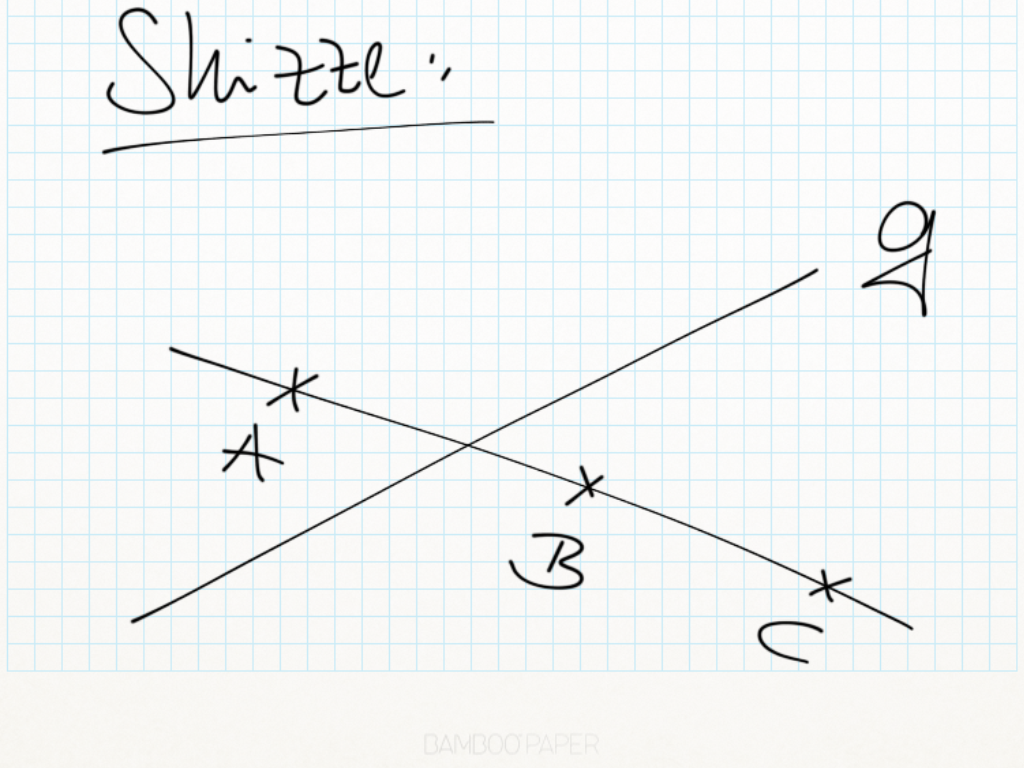
[[Datei:Skizze 7.5.PNG]]<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:14, 12. Jun. 2012 (CEST) | [[Datei:Skizze 7.5.PNG]]<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:14, 12. Jun. 2012 (CEST) | ||
| + | === Lösungsvorschlag Nemo81 === | ||
| + | Vor: koll(A,B,C) und A,B,C <math>\not \in </math>g, <math>\overline {AB}</math> <math>\cap</math> g <math>\neq</math> <math>\empty</math> und <math>\overline {BC}\ \cap\ g = \empty</math> | ||
| − | + | Beh: <math>\overline {AC}\ \cap \ g\ \neq\ \empty</math> | |
| − | + | ||
| − | Beh: | + | |
Bew: | Bew: | ||
| − | 1. koll(A,B,C) und A,B,C | + | 1. koll(A,B,C) und A,B,C <math>\not\in</math> g laut Vor: |
| − | 2. AB+BC=AC laut Ax II/3 Dreiecks ungl. | + | 2. |AB| + |BC| = |AC| laut Ax II/3 Dreiecks ungl. |
| + | *Dieser Schritt stimmt so nicht, da eine der drei Gleichungen gilt und nicht genau diese. Hier muss man die Fälle unterscheiden.--[[Benutzer:Andreas|Tutor Andreas]] 17:04, 21. Jun. 2012 (CEST) | ||
| − | 3. | + | 3. <math>\overline {AB} \cap g = \{S\}</math> laut Vor. |
| − | 4. | + | 4. Zw(A,S,B) laut 3. und trivial |
| − | 5. AS+SB=AB laut Ax II/3 und 4 | + | 5. |AS| + |SB| = |AB| laut Ax II/3 und 4 |
| − | 6. AS+SB+BC=AC laut Rechnen in R, 5. und 2. | + | 6. |AS| + |SB| + |BC| = |AC| laut Rechnen in R, 5. und 2. |
| − | 7. AS+SC=AC laut Rechnen in R und 6. | + | 7. |AS| + |SC| = |AC| laut Rechnen in R und 6. |
| + | *Ist dieser Schritt so gemeint, dass |SB| + |BC| = |SC| ist und das dann eingesetzt? Dafür müsste man aber eigentlich wissen, dass Zw(S,B,C) gilt.--[[Benutzer:Andreas|Tutor Andreas]] 17:33, 1. Jul. 2012 (CEST) | ||
8. Zw(A,S,C) laut 7 und Ax II/3 | 8. Zw(A,S,C) laut 7 und Ax II/3 | ||
| − | 9. Unmittelbar folgt | + | 9. Unmittelbar folgt <math>\overline {AC}\ \cap \ g\ \neq\ \empty</math> weil <math>\overline {AC}\ \cap \ g\ =\ \{S\}</math> laut 8. und trivial q.e.d --[[Benutzer:Nemo81|Nemo81]] 18:55, 14. Jun. 2012 (CEST) |
| + | *Der Beweis scheint mir nicht ganz wasserdicht. Mir fehlen hier und da ein paar Schritte oder Erklärungen. Diese sollten noch ergänzt werden, damit ich den Beweis besser nachvollziehen und evtl. korrigieren kann. --[[Benutzer:Andreas|Tutor Andreas]] 17:35, 1. Jul. 2012 (CEST) | ||
Aktuelle Version vom 1. Juli 2012, 16:36 Uhr
 --KeinKurpfälzer 17:29, 11. Jun. 2012 (CEST) Idee von Wurzel
--KeinKurpfälzer 17:29, 11. Jun. 2012 (CEST) Idee von Wurzel
--Tchu Tcha Tcha 19:14, 12. Jun. 2012 (CEST)
Lösungsvorschlag Nemo81
Vor: koll(A,B,C) und A,B,C 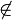 g,
g, 
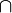 g
g 
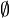 und
und 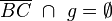
Beh: 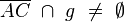
Bew:
1. koll(A,B,C) und A,B,C 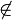 g laut Vor:
g laut Vor:
2. |AB| + |BC| = |AC| laut Ax II/3 Dreiecks ungl.
- Dieser Schritt stimmt so nicht, da eine der drei Gleichungen gilt und nicht genau diese. Hier muss man die Fälle unterscheiden.--Tutor Andreas 17:04, 21. Jun. 2012 (CEST)
3. 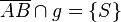 laut Vor.
laut Vor.
4. Zw(A,S,B) laut 3. und trivial
5. |AS| + |SB| = |AB| laut Ax II/3 und 4
6. |AS| + |SB| + |BC| = |AC| laut Rechnen in R, 5. und 2.
7. |AS| + |SC| = |AC| laut Rechnen in R und 6.
- Ist dieser Schritt so gemeint, dass |SB| + |BC| = |SC| ist und das dann eingesetzt? Dafür müsste man aber eigentlich wissen, dass Zw(S,B,C) gilt.--Tutor Andreas 17:33, 1. Jul. 2012 (CEST)
8. Zw(A,S,C) laut 7 und Ax II/3
9. Unmittelbar folgt 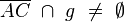 weil
weil 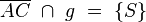 laut 8. und trivial q.e.d --Nemo81 18:55, 14. Jun. 2012 (CEST)
laut 8. und trivial q.e.d --Nemo81 18:55, 14. Jun. 2012 (CEST)
- Der Beweis scheint mir nicht ganz wasserdicht. Mir fehlen hier und da ein paar Schritte oder Erklärungen. Diese sollten noch ergänzt werden, damit ich den Beweis besser nachvollziehen und evtl. korrigieren kann. --Tutor Andreas 17:35, 1. Jul. 2012 (CEST)