Zusatzaufgaben 8 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Zusatzaufgabe 8.3)
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 15: Zeile 15:
 
<br />
 
<br />
  
−
z.z. offene HE sind konvexe Punktmengen
 
−
Vor: offene HE  gP<sup>+</sup>
 
−
Beh: gP<sup>+</sup>
 
−
 
−
direkter Beweis:
 
−
 
−
(1) Q sei ein beliebiger weiterer Pkt, der mit P in der offenen Halbebene gP<sup>+</sup> liegt
 
−
 
−
(2) Es gilt dann: Strecke QP geschnitten mit g = {}; Begründung: Def. Halbebene
 
−
 
−
(3) dann muss folglich für die Punktmenge R Element der Strecke QP gelten, dass diese mit g geschnitten auch = {}; Begründung: (2)
 
−
 
−
(4) Alle Punkte auf der Strecke QP gehören zur offenen Halbebene gP<sup>+</sup>; Begründung: (3)
 
−
 
−
(5) gP<sup>+</sup> ist konvex; Begrüundung: (4)
 
−
 
−
q.e.d.
 
−
 
−
Es müssten jedoch noch weitere 2 Fälle betrachtet werden:
 
−
 
−
1. Dass die 2 Punkte A und B der Punktmenge auf der Trägergerade g liegen
 
−
-> Strecke AB liegt vollständig in g und gehört somit auch zur HE gP<sup>+</sup>.
 
−
 
−
2. Dass ein Punkt A auf der Trägergeraden g liegt und ein Punkt B jedoch in der offenen HE gP<sup>+</sup> liegt.
 
−
-> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf.
 
−
Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP<sup>+</sup>--[[Benutzer:Sissy66|Sissy66]] 00:09, 18. Jun. 2012 (CEST)
 
  
 
== Zusatzaufgabe 8.4 ==
 
== Zusatzaufgabe 8.4 ==

Aktuelle Version vom 17. Juni 2012, 23:15 Uhr

Inhaltsverzeichnis

Zusatzaufgabe 8.1

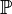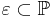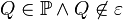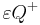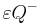Unter dem Raum \mathbb{P}versteht man die Menge aller Punkte. Die Punktmenge \varepsilon \subset \mathbb{P} sei eine Ebene. Gegeben sei ferner \ Q mit Q \in \mathbb{P} \wedge Q \not \in \varepsilon. Definieren Sie die Begriffe Halbraum \varepsilon Q^+ und \varepsilon Q^-.
Lösung von Zusatzaufgabe 8.1_S

Zusatzaufgabe 8.2

Definieren Sie den Begriff Inneres eines Kreises. (Kreis sei bereits definiert.)
Lösung von Zusatzaufgabe 8.2_S

Zusatzaufgabe 8.3

Beweisen Sie: Halbebenen sind konvexe Punktmengen.
Lösung von Zusatzaufgabe 8.3_S


Zusatzaufgabe 8.4

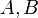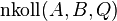Seien A, B und Q drei paarweise verschiedene Punkte für die gelte \operatorname{nkoll}(A, B, Q). Sei g eine Gerade. Beweisen Sie:
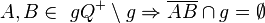A, B \in \ gQ^{+} \setminus g \Rightarrow \overline{AB} \cap g = \emptyset.
Lösung von Zusatzaufgabe 8.4_S

Von „http://geometrie.zum.de/index.php?title=Zusatzaufgaben_8_S_(SoSe_12)&oldid=14995“