Lösung von Zusatzaufgabe 8.3 S: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „z.z. offene HE sind konvexe Punktmengen Vor: offene HE gP<sup>+</sup> Beh: gP<sup>+</sup> direkter Beweis: (1) Q sei ein beliebiger weiterer Pkt, der mit P …“) |
|||
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Vor: offene HE gP<sup>+</sup> | Vor: offene HE gP<sup>+</sup> | ||
| − | Beh: gP<sup>+</sup> | + | Beh: gP<sup>+</sup> ist konvex |
direkter Beweis: | direkter Beweis: | ||
| Zeile 27: | Zeile 27: | ||
-> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf. | -> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf. | ||
Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP<sup>+</sup>--[[Benutzer:Sissy66|Sissy66]] 00:09, 18. Jun. 2012 (CEST) | Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP<sup>+</sup>--[[Benutzer:Sissy66|Sissy66]] 00:09, 18. Jun. 2012 (CEST) | ||
| + | <br /><br /> | ||
| + | *Die Beweisidee ist gut. Ein paar Ungenauigkeiten wie z.B. in Schritt 3: Ist R nun eine Punktmenge? Dann muss man sagen, dass R Teilmenge von <math>\overline {QP}</math> ist.--[[Benutzer:Andreas|Tutor Andreas]] 12:17, 12. Jul. 2012 (CEST) | ||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 12. Juli 2012, 11:17 Uhr
z.z. offene HE sind konvexe Punktmengen
Vor: offene HE gP+
Beh: gP+ ist konvex
direkter Beweis:
(1) Q sei ein beliebiger weiterer Pkt, der mit P in der offenen Halbebene gP+ liegt
(2) Es gilt dann: Strecke QP geschnitten mit g = {}; Begründung: Def. Halbebene
(3) dann muss folglich für die Punktmenge R Element der Strecke QP gelten, dass diese mit g geschnitten auch = {}; Begründung: (2)
(4) Alle Punkte auf der Strecke QP gehören zur offenen Halbebene gP+; Begründung: (3)
(5) gP+ ist konvex; Begrüundung: (4)
q.e.d.
Es müssten jedoch noch weitere 2 Fälle betrachtet werden:
1. Dass die 2 Punkte A und B der Punktmenge auf der Trägergerade g liegen -> Strecke AB liegt vollständig in g und gehört somit auch zur HE gP+.
2. Dass ein Punkt A auf der Trägergeraden g liegt und ein Punkt B jedoch in der offenen HE gP+ liegt.
-> Hierzu teilen wir die Strecke AB in die Strecke AB ohne A und dem Punkt A auf.
Die Strecke AB ohne A hat keinen Schnittpunkt mit g und A gehört zu g und somit auch zur HE gP+--Sissy66 00:09, 18. Jun. 2012 (CEST)
- Die Beweisidee ist gut. Ein paar Ungenauigkeiten wie z.B. in Schritt 3: Ist R nun eine Punktmenge? Dann muss man sagen, dass R Teilmenge von
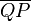ist.--Tutor Andreas 12:17, 12. Jul. 2012 (CEST)
