Lösung von Aufgabe 9.5 S: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 19: Zeile 19:
 
<br />Behauptung stimmt.
 
<br />Behauptung stimmt.
 
<br />qed
 
<br />qed
−
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:57, 20. Jun. 2012 (CEST)
+
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 18:57, 20. Jun. 2012 (CEST)<br />
−
<br />
+
*Völlig nachvollziehbar und meines Erachtens korrekt. --[[Benutzer:Andreas|Tutor Andreas]] 18:36, 1. Jul. 2012 (CEST)
−
== Lösung Kopernikus; Just noch ein sailA ==
+
  
−
==== Vor: ====
+
----
−
<math>\angle ASB ; \ SW^{+}  </math> ist Winkelhalbierende ;  
+
 
−
<br />
+
==== Lösung Kopernikus; Just noch ein sailA ====
−
==== Beh: ====
+
 
−
<math>\angle \left| ASW\right| =\angle \left| WSB \right|  =\angle \frac{1}{2}  \left| ASB \right| </math>  
+
Vor:<math>\angle ASB ; \ SW^{+}  </math> ist Winkelhalbierende ; <br />
−
<br />
+
Beh:<math>\angle \left| ASW\right| =\angle \left| WSB \right|  =\angle \frac{1}{2}  \left| ASB \right| </math> <br />
  
 
{| class="wikitable "
 
{| class="wikitable "
Zeile 59: Zeile 58:
 
| Vor; 5
 
| Vor; 5
 
|-
 
|-
−
 
 
|}
 
|}
 
<br />
 
<br />
 
--[[Benutzer:Kopernikus|Kopernikus]] 19:37, 26. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Kopernikus|Kopernikus]] 19:37, 26. Jun. 2012 (CEST)<br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 19:37, 26. Jun. 2012 (CEST)<br /><br />
 
--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 19:37, 26. Jun. 2012 (CEST)<br /><br />
 +
Ich würde sagen, dass das so passt :) --[[Benutzer:Andreas|Tutor Andreas]] 18:34, 1. Jul. 2012 (CEST)
  
 
== ==
 
== ==
  
−
Kann ich annehmen, dass die Winkelhalbierende im Inneren des Winkels <ASB liegt, oder müsste man beweisen, dass SW+ tatsächlich im Inneren liegt?? Die Definition Winkelhalbierende sagt ja nur aus, "wenn die Halbgerade im Inneren liegt". Ebenso heißt es im Winkeladditionsaxiom "wenn P im Inneren des Winkels liegt". Das Wörtchen "wenn" irritiert mich gerade ein bisschen!  Hoffe mir kann jemand helfen. --[[Benutzer:Mahe84|Mahe84]] 13:23, 27. Jun. 2012 (CEST)
+
Kann ich annehmen, dass die Winkelhalbierende im Inneren des Winkels <ASB liegt, oder müsste man beweisen, dass SW+ tatsächlich im Inneren liegt?? Die Definition Winkelhalbierende sagt ja nur aus, "wenn die Halbgerade im Inneren liegt". Ebenso heißt es im Winkeladditionsaxiom "wenn P im Inneren des Winkels liegt". Das Wörtchen "wenn" irritiert mich gerade ein bisschen!  Hoffe mir kann jemand helfen. --[[Benutzer:Mahe84|Mahe84]] 13:23, 27. Jun. 2012 (CEST)<br />
 +
 
 +
Bin mir ehrlich gesagt auch nicht sicher.. Denke aber, dass wenn ein Strahl die Winkelhalbierende eines Winkels ist, dann muss der Strahl/Halbgerade komplett im Inneren des Winkels liegen (sagt ja die Def. WH auch aus). Von daher müssen dann auch alle Punkte W <math>\in</math> SW+ im Inneren des Winkels liegen...<br />
 +
Das Wort "wenn" sagt ja nur aus, dass "wenn die Halbgerade im Inneren liegt" dann ist es eine notwendige oder sogar hinreichende Bedingung dafür, dass die Halbgerade die Winkelhalbierende des Winkels ist..
 +
Wenn die Halbgerade nicht im Inneren des Winkels liegt, dann ist sie auf keinen Fall die WH des Winkels...<br />
 +
einigermaßen verständlich?? :-) --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:27, 27. Jun. 2012 (CEST)<br />
 +
*Ja, da SW<sup>+</sup> in der VSS die WH ist, muss SW<sup>+</sup> nach Def. WH auch vollständig im Inneren des Winkels liegen.--[[Benutzer:Andreas|Tutor Andreas]] 18:32, 1. Jul. 2012 (CEST)

Aktuelle Version vom 1. Juli 2012, 17:39 Uhr


Satz:
Es sei 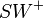\ SW^{+} die Winkelhalbierende des Winkels \angle ASB. Dann gilt:
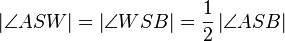
 \left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|

Beweisen Sie den Satz.

Skizze:
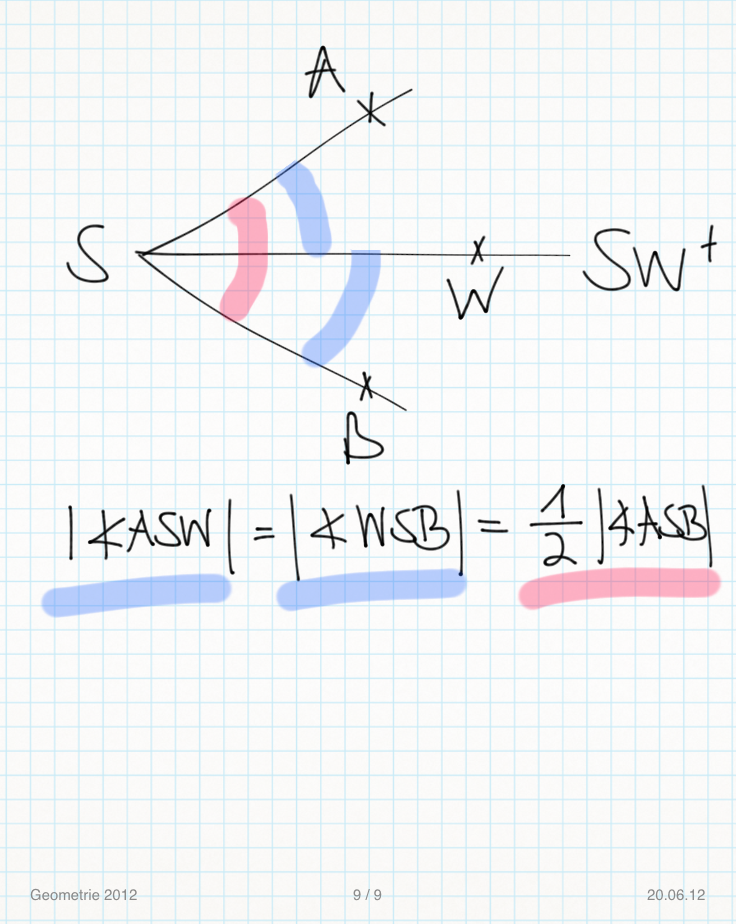
Aufgabe 9.5.png
Voraussetzung 1: \angle ASB
Voraussetzung 2: 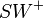\ SW^{+} ist die Winkelhalbierende des Winkels \angle ASB
Behauptung: 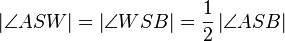\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|


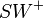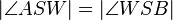
(1) Da nach Vor. \ SW^{+} die Winkelhalbierende des Winkels \angle ASB ist, gilt: \left| \angle ASW \right| = \left| \angle WSB \right|
(2) Nach Vor. und Def. Winkelhalbierende muss W im Inneren des Winkels \angle ASB liegen.
(3) Nun wissen wir nach dem Winkeladditionsaxiom und (1), dass gelten muss: 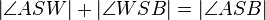\left| \angle ASW \right| + \left| \angle WSB \right| = \left| \angle ASB \right|.
(4) Nach (1) können wir (3) auch folgendermaßen schreiben: 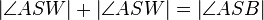\left| \angle ASW \right| + \left| \angle ASW \right| = \left| \angle ASB \right|.
(5) Nach (4) und Rechnen in R folgt: 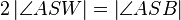2 \left| \angle ASW \right| = \left| \angle ASB \right|.
(6) Nach (5),(1) und Rechnen in R folgt: 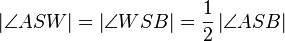\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|
Behauptung stimmt.
qed --Tchu Tcha Tcha 18:57, 20. Jun. 2012 (CEST)

  • Völlig nachvollziehbar und meines Erachtens korrekt. --Tutor Andreas 18:36, 1. Jul. 2012 (CEST)

Lösung Kopernikus; Just noch ein sailA

Vor: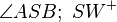\angle ASB ; \ SW^{+} ist Winkelhalbierende ;
Beh: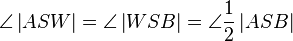\angle \left| ASW\right| =\angle \left| WSB \right| =\angle \frac{1}{2} \left| ASB \right|

Schritt Beweis Begründung
1 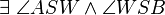\exists \ \angle ASW \wedge \angle WSB Vor; Def. VI1.2 (Def. Winkelhalbierende)
2 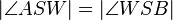\left| \angle ASW \right| =\left| \angle WSB \right| Def. VI1.2 (Def. Winkelhalbierende)
3 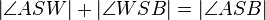\left| \angle ASW \right| +\left| \angle WSB \right| =\left| \angle ASB \right| Axiom IV.3 (Winkeladditionsaxiom)
4 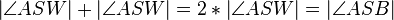\left| \angle ASW \right| +\left| \angle ASW \right| =2*\left| \angle ASW \right|= \left| \angle ASB \right| Rechnen in R
5 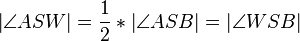\left| \angle ASW \right| =\frac{1}{2} *\left| \angle ASB \right|= \left| \angle WSB \right| Rechnen in R
6 q.e.d Vor; 5


--Kopernikus 19:37, 26. Jun. 2012 (CEST)
--Just noch ein sailA 19:37, 26. Jun. 2012 (CEST)

Ich würde sagen, dass das so passt :) --Tutor Andreas 18:34, 1. Jul. 2012 (CEST)

Kann ich annehmen, dass die Winkelhalbierende im Inneren des Winkels <ASB liegt, oder müsste man beweisen, dass SW+ tatsächlich im Inneren liegt?? Die Definition Winkelhalbierende sagt ja nur aus, "wenn die Halbgerade im Inneren liegt". Ebenso heißt es im Winkeladditionsaxiom "wenn P im Inneren des Winkels liegt". Das Wörtchen "wenn" irritiert mich gerade ein bisschen! Hoffe mir kann jemand helfen. --Mahe84 13:23, 27. Jun. 2012 (CEST)

Bin mir ehrlich gesagt auch nicht sicher.. Denke aber, dass wenn ein Strahl die Winkelhalbierende eines Winkels ist, dann muss der Strahl/Halbgerade komplett im Inneren des Winkels liegen (sagt ja die Def. WH auch aus). Von daher müssen dann auch alle Punkte W \in SW+ im Inneren des Winkels liegen...
Das Wort "wenn" sagt ja nur aus, dass "wenn die Halbgerade im Inneren liegt" dann ist es eine notwendige oder sogar hinreichende Bedingung dafür, dass die Halbgerade die Winkelhalbierende des Winkels ist.. Wenn die Halbgerade nicht im Inneren des Winkels liegt, dann ist sie auf keinen Fall die WH des Winkels...
einigermaßen verständlich?? :-) --Tchu Tcha Tcha 17:27, 27. Jun. 2012 (CEST)

  • Ja, da SW+ in der VSS die WH ist, muss SW+ nach Def. WH auch vollständig im Inneren des Winkels liegen.--Tutor Andreas 18:32, 1. Jul. 2012 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_9.5_S&oldid=15795“