Lösungsideen Übung Heckl A 9 SoSe 2012: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) (→Aufgabe 9.2) |
HecklF (Diskussion | Beiträge) (→Aufgabe 9.2) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | == Aufgabe 9.1 == | ||
| + | Definieren Sie den Begriff ''Inneres eines Dreiecks''.<br /> | ||
| + | <br /> | ||
| + | =Das Innere eines Dreiecks= | ||
| + | Seien ABC drei nichtkollineare Punkte der Ebene <math>\epsilon</math>. Das Innere des Dreiecks ABC kann mittels folgender Applikation dargestellt werden: | ||
| + | <br /> | ||
| + | <ggb_applet width="750" height="407" version="4.0" ggbBase64="UEsDBBQACAAIAGSwz0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAGSwz0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VtbU9tIFn7O/Iouvy6W+35JmUwlJJkwQ5KpSnZra99kqzEKsuRIMuCp+fF7ulu+g8HmMgYKaEl91Jfzndsn2d1fr4YZurBllRb5YYtEuIVs3i+SNB8ctsb1aVu3fn3zS3dgi4HtlTE6LcphXB+2uJNMk8OWIVZQJeO26jPe5kartuF9006EjG1sKbdctBC6qtLXefElHtpqFPftt/6ZHcYnRT+u/cRndT163elcXl5G06miohx0BoNedFUlLQTLzKvDVnPwGoZbuumSeXGKMen89/NJGL6d5lUd533bQm4L4/TNL6+6l2meFJfoMk3qM9gw07SFzmw6OINNKc5bqOOkRqCRke3X6YWt4N6FU7/pejhqebE4d/2vwhHKZvtpoSS9SBNbHrZwRKhWRmtOqVDCKNVCRZnavG5kSTNnZzpa9yK1l2FYd+RnhIXVRZH1Yjci+vtvRDHF6MA1JDQUGilDFw7XMAsNDQ0PjQgyPNzOgygPMjzIcNZCF2mV9jJ72DqNswpUmOanJcA3O6/qSWb9epoL892TA9hTlf4FwgyDnQSdw3WMD9yfhD/uOjrLmyQLs9bleMtJp1MSJuXd56T32imbTar0+pxU3LBPuWHSsPE7bVQs6Bam8r/+b21GtmmbqzOG8/tNKPmTbLHbmfpKt3EPVJ052cZ8ajusnMMwg4Rxdk+QAOeQCsxcIGKgURSBOyAiEBdwSjSSrlWIKejgiCGNnBxhyHuH0PCPKz+YRAIGc1cVOCUiMBFHgiHinYojcCXkHROclDKQEAIJuMlNT6gbgknEJZwxjTis0fmkIiDI4EY4h+kpYgQxdzNRiEok3XiEO1+X2i0dhqRIYiSJGxDcGlw6uDPIa8TcbmSjrjQfjeslFfWHyfSwLkYzLEAaAtI87IUAtRQVX3WzuGczyBTfHJIIXcSZ8wg/0WmR12gKIg3XBmU8Okv71Tdb13BXhX7EF/FJXNurjyBdTef2sv0ir/4si/qoyMbDvEKoX2R4tuYiIwvHdLZqOGELHXyxQyx0yIVjde28BfSgcWVh/qKspuJxkhw7iXloAE1+zbPJu9LG56MiXd5Gt+OTTteO+1mapHH+HzBWN4vTC5rnIBevpjlIKDNdSVEm3yYVmDC6+p8tC4hVkJ8XfyD6TJoebJa7YMSqHzvnE3i5ByLB5IYuEma2FzOE4is73+ygdJ69cHJcvSuy+SW//6N4VI9LXz7A8kq3qbf5ILPeRny4hdzcP+8VV9+aaB3G+j4ZwRkOK+gNvN4RxAYqoHwYNG0vtF7GLW0mhb0M9hJ4am1pMusnhnoJ3/ZC66XAfMPSmq2S6TYJnk6TVj6i4VbjN9No5YzfZfpxntYn05M67Z83WyXhhi/jYc/OTGh5TPJQY3Y7KzbWPbdlbrPGpAHMcTGugocuWHti++kQTkNHo5LYwfVvWEC4mthBaacLz3xpFhTme/Gisa5d9kN9LIvhcX7xHWxhZQHdznSV3apfpiNnc6gHaeDczq0qSasYskiyeJ/zQdh632ULUE/tVAPeOa7PCgD7Y1ZIQCuByAKXnf9ldgj1Fqq9jXkznen6rS/knFJR0fsBwW2W/0L/HDXovtbevGXG2egsdsVes/MsnthySRd+vM9FsqohAMBvAxx95KtFgHhkbbCOsGI4GMGA3qmWYhUovUJXsISIQr6dHLbaNMJw9Fco5UMp67brfG0pPoerK4CBFQVN3aKzd/uls100JiMTFIYjSh9dYUfPX2Es4tprjEQPY2D9YjiM8wTlviQ8gTjcmlcoMXaeiWLijC0oZlxPO+IwVDPAmupdSJ9pNr5F88upP0mDllxWb6SLzbjg3VGZ67ZNIkdDJ45Wu1rAaZdFQrO1JFVD/XQOLLHymbRucqY/+JQmifW1c0jiP/NwSxUyRzocZWk/rTfD8Kc322Uc4jUA3m8GYNn2368jsJztrjd+QkPe9+0+OABECi2xwYpwZoxWlDQRhEVUEKyZwRJTAcfqEfzjbsB82AaYDy8EGAKlL4eyGUvGuTZMNZ4kKIMrRmoN/x8oK66Ckk0GRb4Cy/sQtz5AQ92Dm1WQoEDLoAImQSwJYo5cAHXpQQOspQ8N8JWP0ABV+e02VMMqprDNxr8xdODNoeNhoyV1qr82XrJtbOXmVFvZgTubLTK5e8i/2zp3j+sqUoororXiEDuIkCGDmgiMVRqllOZaYyO8bQodQfzAjMEtGlMuNwT/WxDcFPy9LWbOn47zGkiE9VX0Ojc4t3bkSNnX/HsZ55V78BtkFjjHHRGx+4PIqu51KGquQwog4YRHDGulNYUoAoH9pSDS2xtEVhUf6qBrcQJAmNERXNRMUmUY9L8YRPp7g8haePKIXIOTcxAagY9gTRTTWlCu+LMFZLk4+rgTY5MBDNf0QrNzYTS+SrM0LifLy1/CiURUEahHlTCSGkpCdqE84gyyCAW4GKXGsEent7/tv7LaEDeYkBRMFwzVWXFIxTKSQkjCoJ7nkuqnpbZHa7Xh6RbU9vS+1PbnU1BbFvFG1REF3rTwEyI6wXBdkIXr+8B5T9eQ+bQNtfr0QqiVgKBPMaQBo7DUzC0rpAKhIUEwpY2EavVhnp/tAsrxNqAcvxBQ3BNLTh1B4OAtHFMyLWElxHtYJpFcQPh/mLh/F8b7KYSz41sYLw1iZ0EsDYx3EBjvj8B4fw+M94+dGC/9JxjvjUGUYLoWRvk21nL32vFst9rx5nXuXjuKiBko1ok2ghMFdWKwTREJILVKYkYhkJjmkXubQ4AxDKxZCEJAYtPzzv2uHlchSfcGklXVh2ixBlQTxKEgopRKxowwQnD9fOv5VUQGe4NI+zrlT9aRCsUoI1BCCcKJFExhxl/OQ4gf+4PIqupl8xRiFaiGHwgCHAvcA2NwFSqeb9harpB+338eB4hIIrDmTGJwCU6a997gJERjgApiloAqyDz+W/A/dqsnn1RdlEREUgN2DeFECxa0RSNKMCRexsHWuX6UF1bXsN6jm17onm/Bes/vy3rLJ2C9BIx0ieuGZ2gQyOnSB66CkbaBA0MJtOl5/5MR3/M1cE624VgnL4RjUR4RopSmGgtOjZZNHasjpoQyRAtBMZNEPxH1XYfl8zawfH4hsLRxpDTWhHNlJIN4P/MrMoeKU/FkzPckhLTPtzBfFsSyIDYMzDcPzHcUmO+XwHy/7sR82T/BfK8JpILc+JGlR3rZm+1WQ25Y6D3KegJslmNFmdHEYP8tCv+ZPB5po4VRVAssXZnp7VOJyGD/8qQx52dbRa6CMtwfUNZ0P32/uIpVSMXCREpIoL/AfKFw0i8Hk3x/MFnVvZi+t1pDChCRGip7prWmTFDDCXkxiIz2B5G1ENV81HPVSULgksZEVDMpgBAzoZ7xE4nlKunL/tPfNqERaFxrqZvqdJpjSMQ1ZkQqoBguozxMDbRJXV/3X12gLUaZInhmxM1HNllEFWfaQPqlinDzGNrqFUVm43mtVnh9wZ1ju2bD9/lo+N0Z69fT08rW/qEwx8HDmdkYIeKRL/v8tU8f0Nt3B0f/2m7XP/dx10Jvteujg3db7rrcx12rrbB+d3Twdm3XncVv3vgvuDXf1n7zf1BLBwhfnNePhwoAAEo+AABQSwECFAAUAAgACABksM9A1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAGSwz0BfnNePhwoAAEo+AAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAHgsAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 22:05, 15. Jun. 2012 (CEST) | ||
| + | |||
== Aufgabe 9.2 == | == Aufgabe 9.2 == | ||
'''Satz:'''<br /> | '''Satz:'''<br /> | ||
| Zeile 7: | Zeile 16: | ||
<br /> | <br /> | ||
[[Datei: A_9_3_27062012.JPG | 900px]] | [[Datei: A_9_3_27062012.JPG | 900px]] | ||
| − | <br /> | + | <br /><br /> |
| + | ==={{Schrift_orange|Diskussion}}=== | ||
Ich möchte diese Aufgabe zur Diskussion stellen: Der Beweis mit den gelben 'Berichtigungen' ist lupenrein. <br /> | Ich möchte diese Aufgabe zur Diskussion stellen: Der Beweis mit den gelben 'Berichtigungen' ist lupenrein. <br /> | ||
In der Übung wurde der Beweis aber so geführt, wie er (in weißer Kreide) geschrieben steht. Hierbei wurde mit dem Existenzbeweis der rechten Winkel argumentiert.<br /> | In der Übung wurde der Beweis aber so geführt, wie er (in weißer Kreide) geschrieben steht. Hierbei wurde mit dem Existenzbeweis der rechten Winkel argumentiert.<br /> | ||
Ist das möglich? Ist das nötig? {{Schrift_grün|'''Möge die Diskussion eröffnet sein :)'''}} --[[Benutzer:HecklF|Flo60]] 20:12, 27. Jun. 2012 (CEST) | Ist das möglich? Ist das nötig? {{Schrift_grün|'''Möge die Diskussion eröffnet sein :)'''}} --[[Benutzer:HecklF|Flo60]] 20:12, 27. Jun. 2012 (CEST) | ||
| + | == Aufgabe 9.3 == | ||
| + | '''Satz:'''<br /> | ||
| + | '''Es sei <math>g</math> eine Gerade der Ebene <math>E</math>. Ferner sei <math>P</math> ein Punkt auf <math>g</math>. In der Ebene <math>E</math> gibt es genau eine Gerade <math>s</math>, die durch <math>P</math> geht und senkrecht auf <math>g</math> steht.'''<br /> | ||
| + | Beweisen Sie den Satz.<br /> | ||
| + | |||
| + | <ggb_applet width="1000" height="500" version="4.0" ggbBase64="UEsDBBQACAAIABOg2kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAToNpAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVa4XLjthH+fXkKDJvJpFNbAgiQFO/ky/iSXusZJ3dTX9NM56YdiIQonChSIUFbvrkXyFPkTx+j//ImfZIuAFIiJcsnWbYn9tgGASyxwO63ux8pDb9ZzFJ0KYpS5tmJQ3rYQSKL8lhmyYlTqfHxwPnm5RfDROSJGBUcjfNixtWJw7SkjE8cdzxmGPujY+5H+JjFjB+PhCDHAY2Yz/iAiiByEFqU8nmW/8BnopzzSFxEEzHj53nElVE8UWr+vN+/urrqNap6eZH0k2TUW5Sxg2CbWXni1BfPYbnOTVfUiLsYk/5P35/b5Y9lViqeRcJB+giVfPnFs+GVzOL8Cl3JWE3gwNT3HTQRMpnAoQJ34KC+lpqDReYiUvJSlHBvq2sOrWZzx4jxTM8/s1coXZ7HQbG8lLEoThzco17IGPUpwTT0KPEclBdSZKqWJbXOfrPa8FKKK7usvjIamYNUnqcjrldEnz4hF7sYHemG2MaFxvftFLZjmNrGtQ2zjWdlmL2dWVFmZZiVYdRBl7KUo1ScOGOelmBCmY0LcN+yX6rrVJj91AOr05MjOFMpP4IwxYATa3MYx/hI//nwx/REv3tI0tKqimpPpY1KQr09dLoHnZQ2SllINnW63pZz+rcotQff6aDtc4Iq82v+NjTS2465rtH2D1Pos0c54rDfxMqwDg9UTrRsDR8lZqUOGBoiL9S4J8iD4PADgLmHSAhN4CIIB0Q8xDzokgHydRsgGsAEQxQNkJYjFJno8AbwjwVmMR95sJgeDSAoEQFFDHkUERNUDEEoIROYEKQuBQnPQx7cpNUTVy9BfcR86NEBYrBHHZMBAUEKN0If1LuIEkT1zSRAro98vR5hOtb9gd46LOkiHyOf6AUhrCGkbTiD/ABRfRq/NpfM5pXqmCiaxc2lyudLX4A0JKRV2rMJqpMVnw1TPhIpVIoL7UmELnmqI8IoGueZQo0TXTuWFHw+kVF5IZSCu0r0gV/yc67E4jVIl41uIxvlWfm2yNW3eVrNshKhKE/xcs95SlrX7nLX0KGtCdae8FoTfus6uFFvDjOoKgXoz4uyEedxfKYlVqkBLPkmS69fFYJP57nsHmPYN0VnKKoolbHk2Y8AVq1F2wWtapAGeVODPJ82O8mL+OK6BAijxT9FkZ84odfD7R+IsWs742LanQKHlxHXwefh7gykrOstU8RqFpdLD/GFWB02KXRktzpn5as8XQ2Z83/L56oqDH0ATYU+1GmWpMJgxKRbqM3RdJQvLupsbdd6dz2HHrY7GCXG7ghyg+tBvUzqdmRbI6O3tpTCRgYbCdygTcbLeRK6RsK0I9saKYCv3Vp9VNIck+BGjSxNRsNOHTdNttLg15W+yqQ6bzpKRtP6qMTe8EM1G4klhLprkvtac9hfw9hwKopMpDWkwZlVXpU2Qltoj0UkZ9C1E7VJuHbX32EDdjQWSSGajaeGmlmDmVncBuvGsFnqdZHPzrLLd4CFtQ0M+80uh2VUyLnGHBpBGZiKFapiWXKoInH7Ph2DcPRIVwswj9Kmgeis1CQHZ79Ocx+8FUNmgWEdf6mYAd9CymDMwHRp67eGyGmjonz0AZLbsv7Z+ZXXQGksjUYT9bUwt5Nw741gNLDl6XzCNROszZLya1F0DGWUfZ/H6+YD71iNSsz1Atr/cyEsdOxx4GIOC5qI6yQy8EiJFvquAELeqAd6+9GyfMtytSV0GHZStx1d8yUAzBrxc+b8N9k0aBfdK4v+jo1GaI8OjNlIL7gfs0X5bMazGGWGA51D4nFWJZljDUXEiTWhNU+lmqnELlYvseEDncWW9k12RvQ2++O7W39lwWNS4464PX/QLTPanOCXwPPC1s9gPSUrYAtTeCYqTd1QdYUwF3+VcSwMU7Ql6+fM3lLaPCln81RGUm1AdzEvYD2Njtoa78RCwYZg4sT56ucqVy++RG/ReyRLBf+FzOD/WACUivcI7iigq0mPGMnEdN5W2VRL8moM/5Pel3YRo7jrJOA5qzixam93VJeW7J97DnCjLM/5O/GTHVsBxrC6UhRyvCTxpohjpzF8fT88dxfqrY4IpLHAemyDuABCgLPQDgBoO9A+7zd3zW8/XlygPezvHmr/EfrfL7+iB42ne3YEpDXciTlvb090bDqChy7Bs6XJuDEpbLYSG2TjcTLSm/G4FEqf1XVt/qGef2vGAsKqHWvGLqJJIZVCZL9jjw489pbwvnd4rYzj07A2Dt3ZOK+ACf723yyugKVtGujGCKVrEfrnUidVoL9KikKnzURkvFom2gtV8Emqs+rpv/6kk7AeTOD6COL6DwTDCmUe81Kv8umrVL3QckfJJ3SCQqxFZap6uycAemgCeDJxz4DNrJVgG/Z+N+y3RX2Xu7wpgGgnecbT7Swm2eAw0R4cJvociWy55oFZzA3s5bphN2CssIfJxrPk/ROXrgOMY9fsHm0Y/PR2g3eJ++mBz0E3OIO49tHdtL8PWo97lAZ+yDzfYwPPH4SBrREukHyXBq4bhsEgxCH2HoDy/41f3xwrpxuui293XQErNY6JHyCJEex2XrqY/j0EE5gZd8xcE0Fwi+9S7DHKPMKoUWfMH7rYZx5mzNdvyR7oAcFYPtWoOcuA55fCvFfYfFsyFWKuX1O9yd4VPCv1R2Hd/Lw7YRBPjjAs2VQY7s2m3N3IAlsjC1+TPx5BUf+HzKYindpXPlPjGr6Q+UzP7cn42aGxMn4qBV8T/aBd2oOm4ofdiu/fjeiPHwTA4jEY7x4AbjPeHUHsrYH4u6qIJoDUU/iroBS8N28XLkWR/vafarxGgQU0fxEFj/VF+WLJeddIs11n+YYiFpWSSW+fQPAODYTJUwkEYL6dOPBtHLDeoDO8I/O9ge+e1m/tNmp4uQffLQ9kXw/njlX13lK8t9Tu40cq3runrMmTS1lNzWUs2Lvm0t3Slb9ec12ouWfZRwn2/2jKLOSYsx7ZJ7n4hyYX+VSSi66y7SwS0ia7hN2fuxVZ+SCInTxokbUfmjDP3Rmx7SK7I2qDNdRCgZyLYo6SZXEsNwvkHggODkXw9KkgmPVYhw/WNNFfw/XW8ng7gD88CIDvzbht3NaZ9o7kkO2G28FN2fY9+pqa5jsxlpk9LgBYZNNCRBO1T+YdHIrbD0/xEw1C2lCtXyl46w86d0Pw9MmlYNe1KdjD+3/ssSOMwzUYvxJXQuqMe1qNExCDq7BH9fv8/EJ3XEzcfWAc7g7jrV8h0Oz0kSCqv855K0bd3voH3c0r5M4zyFaW0G9/38V8raz+jvTL/wNQSwcIL1U0zJoJAADALQAAUEsBAhQAFAAIAAgAE6DaQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAToNpAL1U0zJoJAADALQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAADIKAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 15:38, 27. Jun. 2012 (CEST) | ||
| + | |||
| + | == Aufgabe 9.5 == | ||
| + | '''Satz:'''<br /> | ||
| + | '''Es sei <math>\ SW^{+} </math> die Winkelhalbierende des Winkels <math>\angle ASB</math>. Dann gilt:<br /> | ||
| + | <math>\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|</math> '''<br /> | ||
| + | |||
| + | Beweisen Sie den Satz.<br /> | ||
| + | <br /> | ||
| + | [[Datei: A_9_5_27062012.JPG | 900px]] | ||
| + | <br /><br /> | ||
| + | Und für die Freunde eines gepflegten ikonischen Beweises :) : | ||
| + | <br /><br /> | ||
| + | [[Datei: A_9_5_27062012_ikonisch.JPG | 900 px]] | ||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 20:18, 27. Jun. 2012 (CEST) | ||
=Zurück zur Übersichtsseite= | =Zurück zur Übersichtsseite= | ||
Aktuelle Version vom 27. Juni 2012, 19:19 Uhr
Inhaltsverzeichnis |
Aufgabe 9.1
Definieren Sie den Begriff Inneres eines Dreiecks.
Das Innere eines Dreiecks
Seien ABC drei nichtkollineare Punkte der Ebene 
. Das Innere des Dreiecks ABC kann mittels folgender Applikation dargestellt werden:
--Flo60 22:05, 15. Jun. 2012 (CEST)
Aufgabe 9.2
Satz:
Jeder rechte Winkel hat das Maß 90.
a) Formulieren Sie mit "wenn...dann..."
b) Beweisen Sie den Satz.
Diskussion
Ich möchte diese Aufgabe zur Diskussion stellen: Der Beweis mit den gelben 'Berichtigungen' ist lupenrein.
In der Übung wurde der Beweis aber so geführt, wie er (in weißer Kreide) geschrieben steht. Hierbei wurde mit dem Existenzbeweis der rechten Winkel argumentiert.
Ist das möglich? Ist das nötig? Möge die Diskussion eröffnet sein :) --Flo60 20:12, 27. Jun. 2012 (CEST)
Aufgabe 9.3
Satz:
Es sei 
eine Gerade der Ebene 
. Ferner sei 
ein Punkt auf . In der Ebene gibt es genau eine Gerade 
, die durch geht und senkrecht auf steht.
Beweisen Sie den Satz.
--Flo60 15:38, 27. Jun. 2012 (CEST)
Aufgabe 9.5
Satz:
Es sei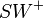 
die Winkelhalbierende des Winkels 
. Dann gilt:
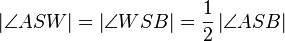
Beweisen Sie den Satz.
Und für die Freunde eines gepflegten ikonischen Beweises :) :
--Flo60 20:18, 27. Jun. 2012 (CEST)
