Übung Aufgaben 9 S (SoSe 12)

Aufgabe 9.1

Definieren Sie den Begriff Inneres eines Dreiecks.
Lösung von Aufgabe 9.1_S

Aufgabe 9.2

Satz:
Jeder rechte Winkel hat das Maß 90.

a) Formulieren Sie mit "wenn...dann..."
b) Beweisen Sie den Satz.
Lösung von Aufgabe 9.2_S

Aufgabe 9.3

Satz:
Es sei $g$ eine Gerade der Ebene $E$. Ferner sei $P$ ein Punkt auf $g$. In der Ebene $E$ gibt es genau eine Gerade $s$, die durch $P$ geht und senkrecht auf $g$ steht.

Beweisen Sie den Satz.
Lösung von Aufgabe 9.3_S

Aufgabe 9.4

Warum ist die folgende Definition des Begriffs Winkelhalbierende nicht korrekt?

Die Halbgerade 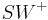$\ SW^+$ ist die Winkelhalbierende des Winkels $\angle ASB$, wenn $| \angle ASW| = | \angle WSB |$.

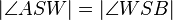Eine Skizze genügt.
Lösung von Aufgabe 9.4_S

Aufgabe 9.5

Satz:
Es sei 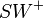$\ SW^{+}$ die Winkelhalbierende des Winkels $\angle ASB$. Dann gilt:
$\left| \angle ASW \right| = \left| \angle WSB \right| = \frac{1}{2} \left|\angle ASB\right|$

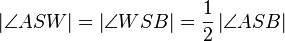
Beweisen Sie den Satz.
Lösung von Aufgabe 9.5_S

Aufgabe 9.6

Im Skript zur Dreieckskongruenz finden Sie einen Beweis für den Kongruenzsatz WSW ("der fotografierte Beweis").
a) Vollziehen Sie diesen Schritt für Schritt nach.
b) Beschreiben Sie in Ihren eigenen Worten die Idee, die hinter dem Beweis steckt. Formulieren Sie möglichst einfach, wie der Beweis geführt wird.
Der fotografierte Beweis
Lösung von Aufgabe 9.6_S

---

Lösungsideen Übung Heckl A 9 SoSe 2012